GTOソルバーは、可能な限り最も優れたポーカー戦略を計算するアルゴリズムです。しかし、ソルバーは一体どのように動いているのでしょうか。どのように最も優れた戦略を計算しているのでしょうか。
この記事では、ソルバーがどのような仕組みで出来ており、ソルバーは何を生み出しているのか。そしてソルバーの限界について深く掘り下げていきます 🏄♀️
ゴール
まず初めに、以下の2つの記事を紹介します。ソルバーについて知らない方は以下の2記事を先に読み、基本的な知識を習得することをおすすめします。
ポーカーにおけるGTOとは?そしてGTOはどこを目指しているのか?GTOの目的はエクスプロイトできないナッシュ均衡戦略を立てることです。
ナッシュ均衡とは、どのプレイヤーも自らの戦略を変更しても、これ以上多くの利益を得ることができない状態のことを指します。つまり、自身の戦略を公開したとしても相手は追加で利益を得られないということです。しかし実際にソルバーは「ナッシュ均衡」の意味を知っているわけではありません。
ソルバーのゴールはただ1つ、利益を最大化することです 💸しかし相手もエクスプロイトしようとしてくるため、両者は互いにエクスプロイトし合いながらどちらもエクスプロイトしてもこれ以上利益がでない地点に達するまで計算します。これが均衡です ☯︎
GTOは、エクスプロイト的なアルゴリズム同士を、どちらもそれ以上エクスプロイトできなくなるまで戦わせることで戦略を構築しています。
GTOのメカニズム
- 各プレイヤーにランダムな戦略を割り当てます(各決定点における各アクションの可能性は等しいとします)。
- ゲームツリー全体を通して、相手の戦略に対するEVの後悔(regret)を計算します。
- 相手の戦略を固定したまま、一方のプレイヤーの戦略を変えて、後悔を減らします。
- ステップ2に戻って後悔を再計算し、後悔を減らすために相手プレーヤーの戦略を変更します。
- ナッシュまで繰り返す。
これらの各サイクルは反復と呼ばれます。必要な反復の回数は、ツリーの大きさやサンプリング方法によって、数千回から数十億回まで様々です。
ステップ1)ゲームスペースを定義する
インプット
ポーカーを直接解くには複雑すぎるので、部分集合と抽象化を使用してゲームスペースを縮小する必要があります。
一般的に、ソルバーを実行するには、以下のパラメーターを定義する必要があります。
- ベットツリー
- 必要な精度
- 最初のポットとスタックサイズ
- レンジ(ポストフロップソルバー)
- ボード(ポストフロップソルバー)
- カードバケツやNNs(プリフロップソルバー)などのポストフロップのカードの抽象化
- レーキやICMなどの効用関数の調節
ベットツリーの複雑さ
ゲームツリーのサイズを小さくするために、使用するベットサイズを定義する必要があります。アルゴリズムを理解するには、まず「ベットツリー」がどのようなものか理解する必要があります。ソルバーは提供されたパラメータ内で動作します。ソルバーに非常に単純なゲームツリーを与えると、簡単な戦略が生まれますが、ソルバーはゲームツリーの少なさをエクスプロイトしようとします。
ソルバーは、設定されたベット(サイズや数)で可能なすべてのラインを含む「ツリー」を生成します。ツリー全体の各決定点には「ノード」が含まれます。例えば、あるプレイヤーがベットをされた時、それは1つの「ノード」となります。ツリー内のノードの数は、ツリーの大きさを定義します。各ノードはそれぞれ最適化する必要があります。
下記のように極めて単純なツリーでも、最適化しなければならないノードは696,613個あります。
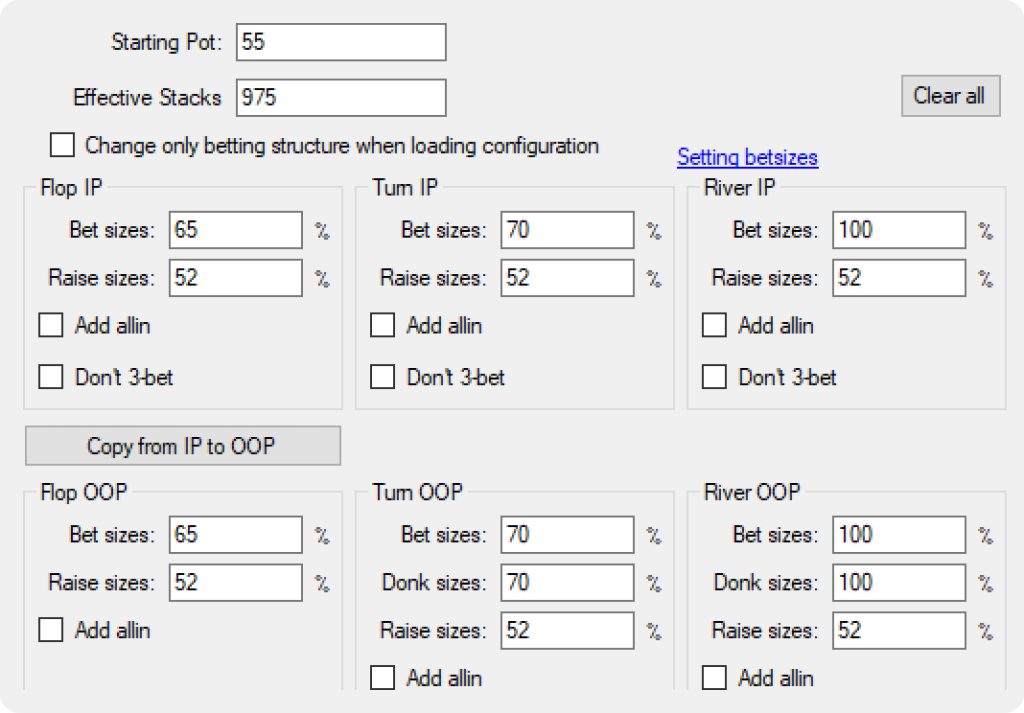
GTO Wizardが使用しているより複雑なツリーでは~87,364,678個のノードがあります。
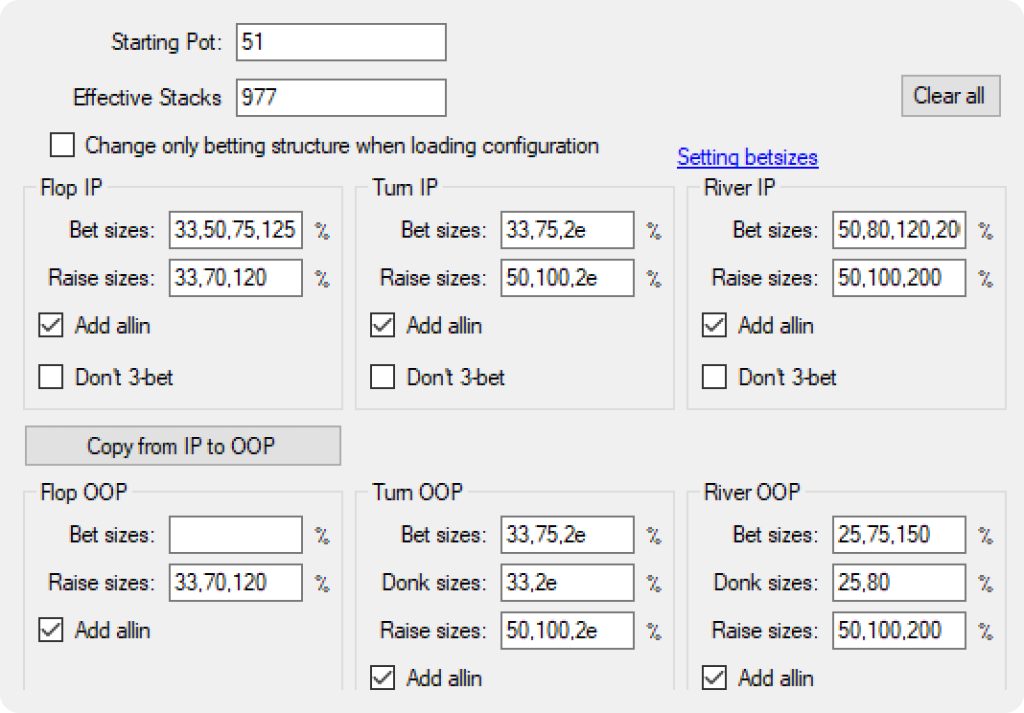
ご覧の通り、複雑にするとツリーは指数関数的に増えていきます。上記の複雑なツリーは、1ノードあたり4~5倍使用しており、合計で125倍も大きく、解くのはより難しくなります。そして、これでもまだ真のゲームスペースを大幅に単純化しています。
ソルバーで最も難しい問題の1つは、現在の技術の制約の中で可能な限り正確な戦略を生み出すためにベットツリーを最適化することです。ツリーを大きくするとその大きさゆえに解けなくなってしまいます。ソルバーがツリーの限界をエクスプロイトし始めるまでツリーを小さくします。私たちはポーカーを研究しやすくするために、簡略化されたベットツリーを見つけるアルゴリズムに取り組んでいます。これらのソリューションは、すべてのスポットで最適なサイズを見つけています。
GTO Wizardには、最大19のサイズを持つ複雑なソリューションからわずか数サイズのシンプルなソリューションまで、さまざまなタイプのソリューションがあります。最終的には、複雑なツリーから始めて、頻度の低いサイズを削除して、より小さく管理しやすいツリーにするのがよいでしょう。
ノードロック
ノードロックとは、あるプレイヤーの戦略をゲームツリーのあるノードで固定することです。そのプレイヤーに特定のプレイをするよう強制します。ノードロックは、エクスプロイト的な戦略を生み出すためによく使われます!例えば、フロップでレンジベットをするように強制すれば、相手プレイヤーはその戦略を最大限にエクスプロイトします。しかし、そのロックされたノードに対応するために、その前後で両プレイヤーが調整し、ターンやリバーの戦略も変化します。

ソルバーに悪いプレイをさせた場合、ソルバーはそのダメージを最小限に抑えるために、前のノードと後のノードを軌道修正します。
1つのノードをロックし、ソルバーにその後悔を回避させるプロセスは、「MinES」として知られています。ツリー全体のリークをモデル化しているのではなく、ツリーの特定のポイントだけをモデル化しています。
より複雑なノードロックもできます。例えば、ソルバーによっては、あるノードで特定の組み合わせの戦略をロックすることができます(他の組み合わせは戦略を調整させる)。また、相手の戦略の大きな傾向を再現し、それをエクスプロイトするために、多くのノードをロックすることも可能です。しかし、最近のツールは複数のストリートにまたがるノードロックには対応していません。
ステップ2)ゲームツリーを解こう!
ゲームツリーを定義したところで次は実際に解いてみましょう。それにはまず、ソルバーがどのように戦略の期待値を計算するのかみていきます。
ソルバーはどのようにEVを計算するのか

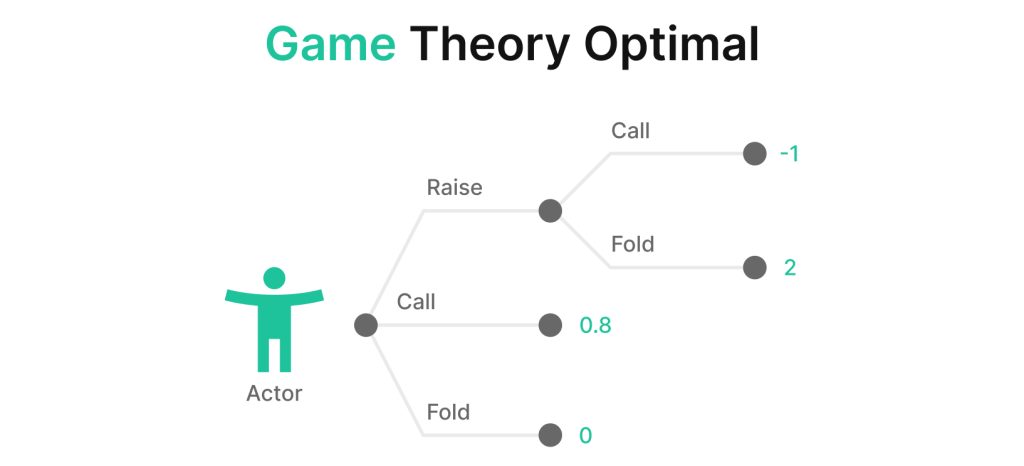
上のゲームツリーを思い浮かべてみましょう。各ドットはノードまたは決定点を表します。それぞれのノードで、それぞれのハンドがどれだけのEVを生み出すか、どうやって知ることができるのでしょうか。
手順は簡単です(コンピューターにとっては)。まず、ターミナルノード(別名リーフノード)を定義します。これは、誰かがフォールドしたり、ハンドがショーダウンになったりして、ハンドが終了したポイントのことです。
各ターミナルノードには確率(p)と値(x)が割り当てられます。レンジの各ハンド(i)は、各ターミナルノードに到達する別々の値と確率を生成します。各ターミナルノードの値と確率を掛け合わせ、それらを合計して期待値を求めます。各ノードの値は、勝ったポットの合計から、そのポットに投資した金額を引いたものとして定義されます。
- 戦略ペアから始めます。
- こちらの戦略と相手の戦略に基づけば、こちらのハンドはこの頻度(p)で各ターミナルノードに到達します。
- 各ターミナルノードの値をxとします。
- 各ターミナルノードのx*pの合計が期待値(EV)になります。
- この計算を、すべてのノードのすべてのハンドに対して行います。
E [X] = Σxip(xi)
xi= Xが取る値
p(xi) = Xが値xiを取る確率
ソルバーはこの計算をほとんど瞬時に行うことができます。ソルバーが登場する前は、CREVのようなプログラムがEVの計算に使われており、ユーザーが各ノードで戦略を定義しなければなりませんでした。そのため後のノードを純粋なエクイティ計算に落とし込んでおり、全く正確ではありませんでした。
GTO Wizardでは全てのハンドの期待値をみることができます。例えば、NL50キャッシュゲームでのBTN対BB、SRPで、各ハンドの期待値を見ることができ(ストラテジードロップダウンを使用)、個々のハンドにカーソルを合わせると、取り得る様々なアクションのEVが表示されます。
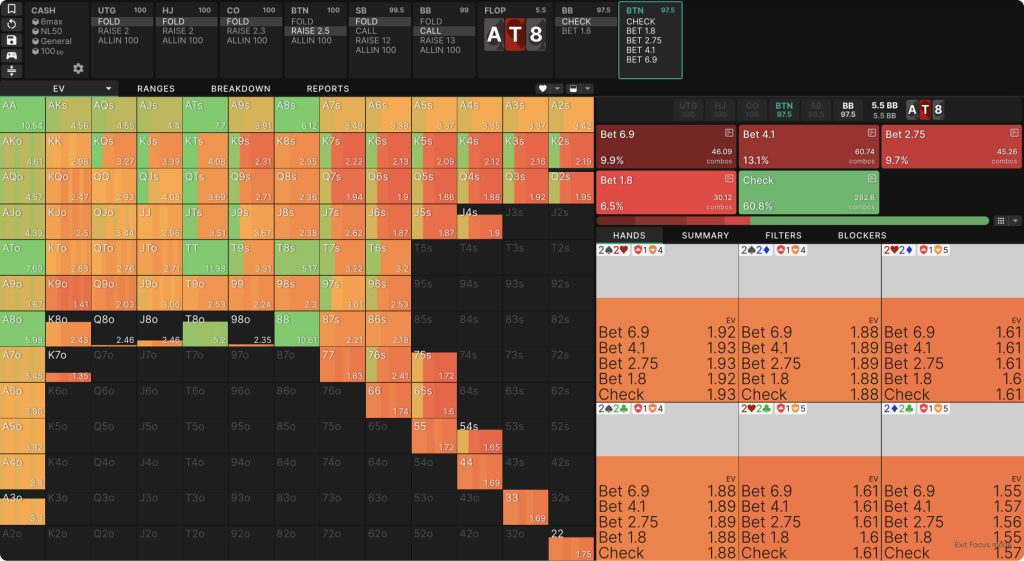
後悔(regret)
各ノードでの各ハンドの価値がわかったところで、どうすれば戦略を改善できるのでしょうか。
ここで「後悔(regret)」という概念が登場します。後悔とは、相手の現在の戦略に対して最適ではない手を打つことによって、どれだけ損をするかということです。
例えば、ベットをコールすることに1の価値があり、レイズすることに3の価値がある場合、コールすることの後悔は3-1=2です。
まず、相手の戦略は固定(不変)であると仮定します。次に、ゲームツリー全体の各ノードでハンドが取りうるすべてのアクションについて、前述のEV計算をします。次に、各点で最もEVの高い点を選択し、最初の点から異なるアクションのEVを計算するために、ターミナルノードから逆算します。

Regret = Action EV – Strategy EV
例えば、現在のハンドの戦略がフォールド、コール、オールインがそれぞれ3分の1で、それぞれのアクションのEVが(フォールド=0bb、コール=7bb、オールイン=5bb)の場合、現在の戦略のEVは次のようになります。
(⅓ x 0) + (⅓ x 7 bb) + (⅓ x 5bb) = 4bb
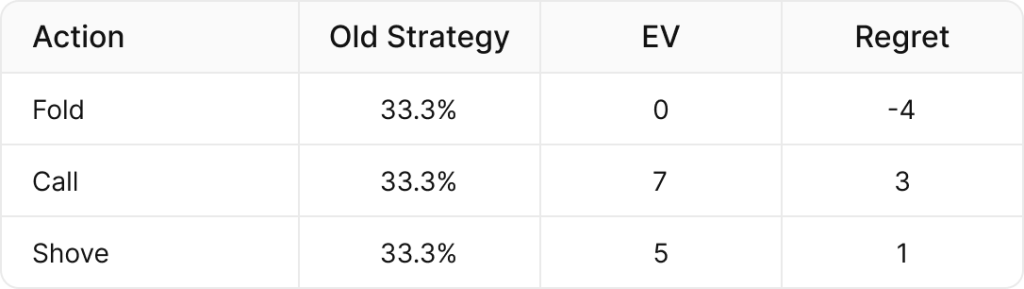
- フォールドは負の後悔(regret)、つまり平均的な戦略よりも負けまています。
- コールとオールインは後悔(regret)がプラスになり、現在の戦略より優れています。
次のステップは、後悔を最小化するために戦略を変更することです。
最もわかりやすいアプローチは、すべてのハンドについて、各決定点で最もEVの高いアクションを選択することです。これはMESとして知られています。このアプローチの問題点は、戦略がループにはまり込む可能性があることです。
例えば、リバーで、プレイヤーAのブラフが足らない場合、プレイヤーBがブラフキャッチャーを全てフォールドし、プレイヤーAが常にリバーでブラフをし、プレイヤーBがブラフキャッチャーを全てコールし、プレイヤーAがリバーでのブラフを止めるといったことを永遠に繰り返します。各プレイヤーは、各反復で最良の反応に全面的に切り替える代わりに、その方向に一歩ずつ穏やかに戦略を調整することができます。これにより、ループにはまる問題が解決され、戦略ペアが均衡に近い場合はよりスムーズに収束します。

後悔を最小化することは、すべてのGTOアルゴリズムの基本です。最も有名なアルゴリズムはCFR – counterfactual regret minimizationと呼ばれるものです。後悔で計算される値は反実仮想値と呼ばれ、相手の現在の戦略に対する確率(反実仮想)で重み付けされた、あるノードでアクションをプレイする値です。
New strategy = Action Regret / Sum of positive regrets
この例では、コール ->3/(3+1) = 75%、オールイン ->1/(3+1) = 25%となり、フォールドはは負の後悔(regret)があるため0%となります。
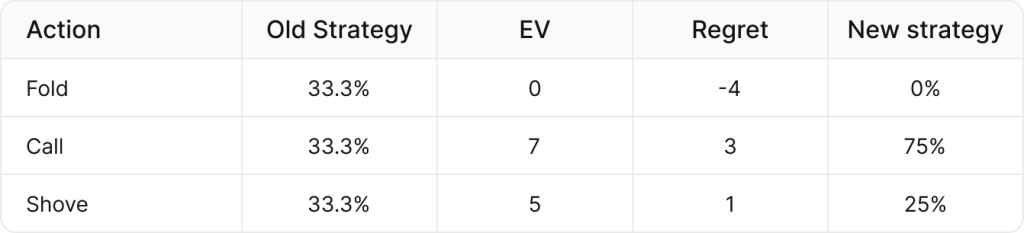
現在の戦略のEV = 4.0
新しい戦略のEV = 6.5
これは1回の反復に過ぎず、このプロセスを何度も繰り返すうちに、戦略はどちらのプレイヤーも改善できない点に近づき、ナッシュ均衡となります。
精度
解の正確さはナッシュディスタンスで測られます。まず下記の質問を考えてみてください。
プレイヤーBの現在の戦略を最大限にエクスプロイトした場合、プレイヤーAはどれだけ勝つことができるでしょうか。
コンピュータはすでに後悔(regret)を知っているので、これを計算するのは簡単です。プレイヤーAの現在の戦略のEVと、彼らのMESとのEVの差は、彼らのナッシュディスタンスを表します。この数値が小さければ小さいほど、エクスプロイトされにくく、正確な戦略であることを意味します。
これらの正確なナッシュディスタンスの測定は、各反復ごとに戦略全体を列挙している場合にのみ機能します。ほとんどのプリフロップソルバーでは抽象化とサンプリング法を用いているため、このような計算は非現実的で不正確になります。HRCやMonkerのようなソルバーは、戦略や後悔が反復ごとにどれだけ変化するかを測定することによって収束を推定しています。
GTO戦略は1%ポット以下のナッシュディスタンスで収束し始めます。このしきい値を超えると、戦略は極端にまちまちになり、信頼できなくなる傾向があります。ほとんどのプロは、0.5%ポットより悪いものは受け入れられないと考えています。GTO Wizardはソリューションの種類にもよりますが、開始ポットの0.1%から0.3%の精度で解いています。ゲームツリーが複雑になればなるほど、似たようなベットサイズを区別するために、より高い精度が要求されます。似たようなベットサイズは似たような演算になるため、ベットサイズが多く複雑なゲームツリーほど、収束させるために高い精度が必要になります。
凸演算空間
この反復アプローチがうまくいくことをどうやって知れるのでしょうか。極大値から抜け出せないのでしょうか。ポーカーは一般に、「双線形鞍点問題」と表現されます。演算空間は次のようになります。
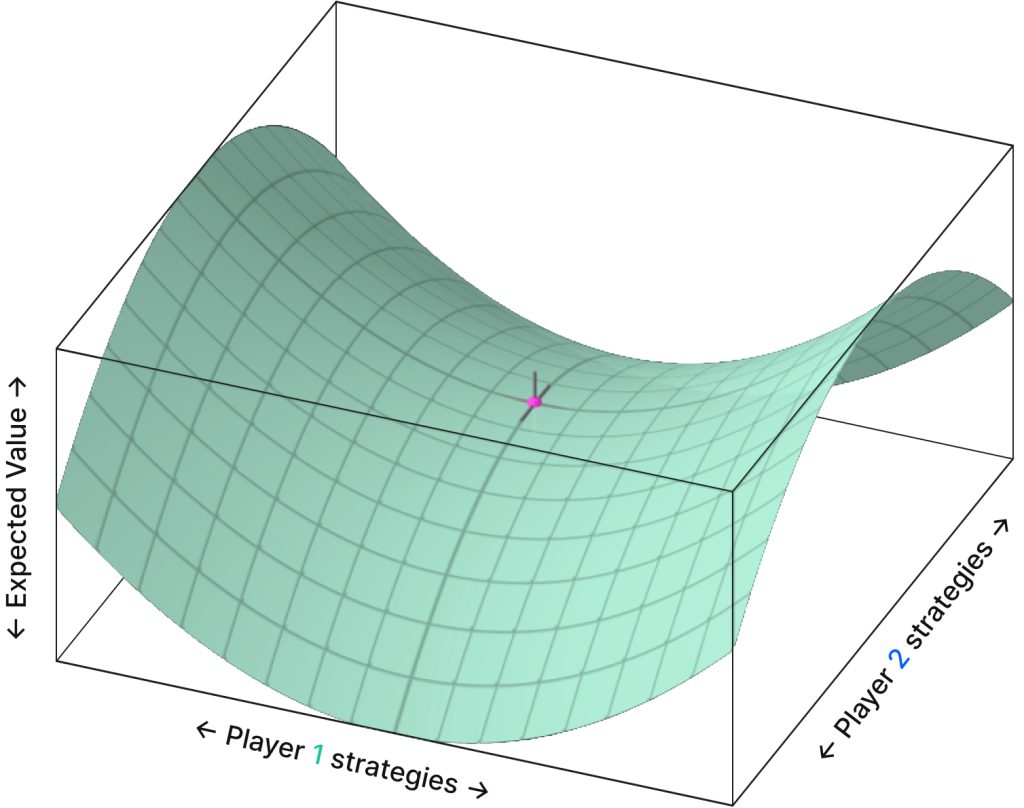
- X軸とY軸の各ポイントは戦略ペアを表します。各戦略ペアには、両プレイヤーが全てのランアウトに渡って(今後出てくるコミュニティカードのこと)、全てのスポットで全レンジをどのようにプレイするかについての情報が含まれています。
- 高さ(z軸)は戦略ペアの期待値を表し、ポイントが高いほど一方のプレイヤーにとってEVが有利であり、ポイントが低いほど他方のプレイヤーにとって有利であることを表します。
ほとんどのソルバーは、Counterfactual Regret Minimization(CFR)と呼ばれるプロセスを使用しており、このアルゴリズムは、Martin Zinkevichによる2007年のアルバータ大学の論文で初めて発表されています。その論文では、CFRアルゴリズムがある極大値で行き詰まることはなく、十分な時間があれば均衡に達することが証明されています。
この鞍の中心はナッシュ均衡を表しています。このグラフ上で、ひずみのない点はどちらのプレイヤーも戦略を変えることで利益的にはこれ以上ならない点を意味します。
より深く知りたい人へ 📚 📚 📚
- ポーカーにおけるCFRについて詳しく知るには、この記事を読むことを強くお勧めします。
- このウェブサイトは、シンプルなCFRアルゴリズムを構築するための素晴らしいチュートリアルと一歩ずつ手順を紹介しています。
- ポーカーにおけるCFRの使用に関する学術資料。
- Deep CFR – CFRの計算を高速化するためにニューラルネットワークを適用しています。
- Improving the original CFR algorithm with “Discounted” regret minimization.
まとめ
ソルバーが実際にどのように機能するのか理解できたかと思います。要点をまとめると、
- 実用的な目的で言えば、ソルバーとは我々が提供するゲームツリーを使ったEV最大化アルゴリズムです。
- ソルバーのアルゴリズムはMESを生成します。これらのアルゴリズム同士を戦わせることで、エクスプロイト不可能な均衡戦略が生まれます。
- 戦略ペアの期待値を計算するのは (コンピューターにとって)簡単なことです。戦略を正しい方向に誘導し、このプロセスを数え切れないほど繰り返すことが難しい部分です。
- ポーカーを直接解くのは複雑すぎるので、ベットサイズを制限するなどの抽象化技術を使ってゲームスペースを単純化します。
- ソルバーは、与えられた抽象的なゲームと同じ精度でしかありません。複雑すぎると解くことが不可能になり、人間がそこから学ぶことも難しくなります。単純すぎると、ソルバーはそのゲームツリーの限界をエクスプロイトしようとします。





