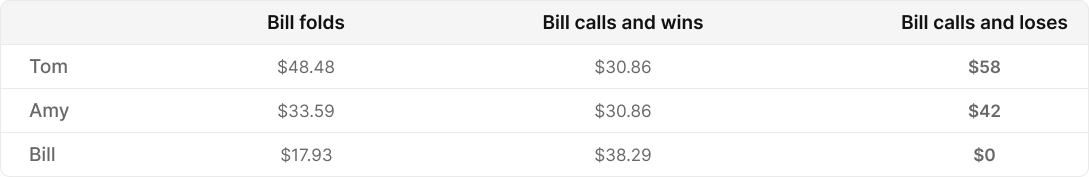トーナメントプレイヤーであれば一度は「ICM」という概念について聞いたことがあると思います。この記事ではICMの基本についてご紹介します。
ICM (Independent Chip Model) とは、トーナメントスタックを実際の金額に換算する方法のことです。1987年にMason Malmuthによって初めてポーカーに使われました。
このモデルでは、スタックの大きさだけでプレイヤーがそれぞれの順位（1位、2位など）でフィニッシュする確率を計算し、その順位の賞金に基づいてトーナメントエクイティを割り当てます。
トーナメントエクイティとは、ペイアウトストラクチャーや自分の現在の順位、スタックサイズを考慮した上で、残りの賞金がどのように分配されるか予想したものです。
ICMの存在意義とは
キャッシュゲームでは、全てのチップの金銭的な価値は、チップの量に比例します。例えばスタックが2倍に増えれば、チップの価値も2倍になります。
しかしトーナメントでは、チップの価値はチップの量には比例しません。スタックが2倍になってもスタックの金銭的な価値は2倍にはならないのです。
チップの価値がチップ量と比例しないため、トーナメントではスタックを金銭的な価値と結びつける必要があります。戦略的な判断を下すためには、チップの増減でEVがどのように変化するか知る必要があります。チップEVを$EVに変換する式が必要です。
そこで、ICMの出番です。
ICMの計算方法
ICMでは、すべてのプレイヤーのスキルが等しいのが前提で、勝つ確率はシンプルにスタックサイズを基準にしています。
ICMは、各プレイヤーが1位、2位、3位などになる確率を計算し、その確率にそれぞれの順位の賞金を掛けます。
プレイヤーが1位になる確率は、そのプレイヤーのチップを全てのチップの総量で割れば簡単に計算できますが、2位と3位の確率は、より複雑な計算が必要です。
例
Tom、Amy、Billが参加人数3人のSnGをプレイしています。スタックと賞金は以下の通りです：
プレイヤーのトーナメントエクイティとは?
まずは1位のエクイティを計算してみましょう。この計算はとても簡単です。優勝する確率は、単純にスタックをプレイ中のチップの総量で割れば計算できます。その確率に1位の賞金を掛けると、1位のエクイティが出せます。
合計チップは1000枚あるとします：
続いて、2位のエクイティを計算します。このステップは先ほどより複雑ですが、手計算でも可能です。2位の確率を計算するには、以下のステップで行います：
- プレイヤーのうち1人が勝ったとして、そのプレイヤーのチップを合計から外し、自分のチップを残っているチップの合計で割ります。
- 1位を取る全てのパータンで、1.を繰り返します。
- それぞれの結果に、他のプレイヤーが1位で勝つ確率を掛けます。
実際に計算してみましょう。
2位のエクイティ: Tomが1位の場合(50%)
2位のエクイティ: Amyが1位の場合(30%)
2位のエクイティ:Billが1位の場合: (20%)
次に、2位のエクイティにそれぞれのパターンが起こる確率をかけます。
2位のエクイティの合計
これで、1位と2位のエクイティを単純に足せば、トータルのエクイティを計算することができます。
ご想像の通り、プレイヤーの人数や賞金が増えるにつれ、この方法は指数関数的に複雑になります。幸いなことに、手軽で簡単なICMの計算ができるツールがネット上にたくさんあります。
複雑すぎるので、プレイ中にICMを計算することはほぼ不可能です。トーナメントのプロはICMを使うスポットをたくさん研究し、さまざまな状況をプレイすることでICMの直感を鍛えています。
先ほどと同じ計算を無料のICMの計算ツール(Holdem Resources Calculator)でやってみましょう。
トーナメントエクイティ
Prizes
活用方法
戦略にどのような影響があるか考えてみましょう。AmyがBTNでフォールド、TomがSBでオールイン、ビルがBBでコール。TomもしくはBillが勝った場合、彼らのトーナメントエクイティはどうなるでしょうか？ICM計算ツールにスタックサイズを入力すれば計算可能です。
Tomが勝った場合
Tomのエクイティは$58 (+$12.82)
Billのエクイティは$0 (-$22.57)
Billが勝った場合
Tomのエクイティは$30.85 (-$14.33)
Billのエクイティは$38.29 (+$15.72)
つまり、Billは$15.72を獲得するために$22.57のリスクを負っており、Tomは$12.82勝つために$14.33のリスクを負っています。ICMではショートスタックは比較的不利になります。Billはこの状況ではより多くのトーナメントエクイティのリスクを負っているため、BBのディフェンスレンジは強くしなくてはなりません。これがトーナメントでスタックが大きい方が有利になる理由です。
リスクプレミアム
簡単にまとめると、勝ったチップの価値は負けたチップの価値よりも低いということです。この同じではないリスクとリターンの比が、「リスクプレミアム」になります。チップとEVをシンプルに計算した結果よりも多くのリスクを負っているのです。
合計した必要なエクイティ
上の例を使って、Tomのオールインを受けたBillのリスクプレミアムを計算してみましょう。ブラインドは25/50で、BBのBillがSBのTomのオールインを受けているとします。
単純なポットオッズの計算で、キャッシュゲームでBillがコールするのに必要なエクイティが分かります。この金額を「チップエクイティ」と呼ぶことができます。
Tom: 500チップ Bill: 200チップ
Billがコールするには追加で150チップ必要で、勝てばスタックは400となります。150 / 400 = 37.5%ですので、 キャッシュゲームでは、BillはTomのレンジに対して少なくとも37.5%のエクイティがあるハンドをコールすべきです。
しかし、先ほど説明したように、得るチップと失うチップの価値は同じではありません。Billはフォールドのコストとコールのリスクを比較する必要があります。Billがフォールドする場合、コールして勝つ場合、コールして負ける場合の3つの状況があります。それぞれの場合のトーナメントエクイティは以下の通りです。
Billがフォールドした場合$17.93のトーナメントエクイティを残せます。Billが$17.93をリスクに晒してコールした場合、勝てば$38.29相当のスタックになります。
新しいポットオッズで計算をしてみましょう：$17.93 / $38.29。つまり、Billがコールするのに必要なエクイティは約47%になります！
ICMの影響で、Billはさらに12%のエクイティが必要になりました。この追加の12%が彼のリスクプレミアムになります。この余分なリスクプレミアムにより、SBのTomは、Billがポットのオッズに対して常にオーバーフォールドしなければならないため、より大きくオープンすることができます。これが大きいスタックの有利な理由です。
リスクプレミアムは、テーブルのそれぞれのチップの量やスタックの合計によって変化します。しかし、以下のような結論になる場合が多いでしょう。
リスクプレミアムは、カバーされている場合は高くなり、カバーしているときは小さくなる。
全体的な傾向と効果
ゲーム中にICMの計算を行うことはできません。しかし、テーブルの外でこれらの影響を研究することで、ゲーム中の直感が鍛えられます。いくつか覚えておくと良い考えを紹介しておきます。
- トーナメントではキャッシュゲームよりもタイトなレンジでオールインする。
- ギリギリのスポットを避ける。トーナメントでは、+cEVのギリギリのスポットは通常-$EV。
- 中くらいのスタックはバブル付近ではタイトにプレイする。
- スタックが大きい場合、オールインのリスクが少なくなるため、ショートにプレッシャーを与えられる可能性がある。特にバブル付近。
- チップを得る価値は、同じ量のチップを失う価値より小さい。
- 賞金配分に注意する。大きな賞金の変動は、リスクプレミアムが高くなる要因になる。
- ショートスタックが飛びそうになったり、ペイジャンプの直前は、チップリーダー以外のプレイヤーは多くの場合強くタイトにするべき。
ICMの限界
ICMは実際のプレイにおける数値化しにくい要素の多くを無視した、純粋な数学に基づいた理論であるため、限界があります。こちらもいくつか覚えておくべきことを紹介しておきます。
- ICMはすべてのプレイヤーのスキルが同じだと仮定している。実際は上手いプレイヤーは、そのスタックサイズから導く勝率よりも高い割合で勝てる。
- 大規模なトーナメントにおけるICMの計算は困難。近年のアルゴリズムはこの分野で進歩を遂げていますが、大規模なMTTでICMを正しく計算するのはまだ非常に困難。
- ICMはプレイヤーのポジションを考慮していない。実際にはスタックが3BBの場合、BBよりもBTNの方がはるかに価値がある。
- ICMはブラインドアップを無視している。ブラインドアップの直前、特にショートスタックのプレイヤーが関わる場合は最適戦略に影響を与える可能性がある。
- ICMはチップリーダーのアドバンテージを過小評価しています。スタックが大きい場合はICMによってショートのプレイヤーにプレッシャーをかけることができるため、ICMよりもビッグスタックのプレイヤーの勝率が高くなる。
代わりのモデル
こういった問題を解決するため、いくつかの代わりのモデルが存在します。
最も有名なものの1つはフューチャーゲームシミュレーションというもので、基本的なICMを改良したものです。ポジションやブラインドの増加、将来のプレイを考慮して、その数ラウンド前から計算します。このモデルは通常のICM計算と併用することで、トーナメントのエクイティをより実際の価値に近くさせることができ、ほとんどのトーナメントソフトの定番とされています。
ICMはビッグスタックの優位性を過小評価するため、それに対処したDCMというモデルもあります。しかし、このモデルは複雑で、ショートスタックのアドバンテージを過大評価する傾向があります。
まとめ
ICMはスタックと賞金をトーナメントエクイティに変える複雑な方法です。この計算はゲーム中はできませんが、テーブル外でICMを勉強することで、より有利に立ち回ることができます。
ICMはトーナメントでのプレイにおいて最も重要な要素の1つである「生き残る価値」を表しています。
トーナメントで重要なのはBB/100ハンドを最大化することではなく、トーナメントエクイティを最大化することです。このような概念を勉強すれば、直感よりタイトにプレイすべき場面や、予想よりもルーズにプレイすべき場面があることに気づくはずです。トーナメントで生き残りたいというプレッシャーを上手に利用し、ICMを考慮して、利益をしっかり確保していきましょう。
翻訳：森 大維河
