ICMの理論的革新

本日は、ICMの誕生以来、トーナメント理論における最も重要な進歩のひとつをご紹介します。

私たちは、従来よりもはるかに短時間でICMスポットを解くことができ、しかも圧倒的な精度を誇る画期的な新しいICM計算手法を開発しました。この技術をGTO Wizard AIに統合したことで、数千人規模のプレイヤーが残っている状況でも、ポストフロップのICMスポットをわずか数秒で解析できるようになりました。

ICMとは（簡単なおさらい）

トーナメントでは、チップの価値は一定ではありません。キャッシュゲームと異なり、トーナメントにおけるチップは「生き残るための手段」であり、できるだけ上位入賞を目指すためのものです。そのため、チップを増やすこと（チップEV戦略）と賞金を得ること（ICM戦略）という2つの目的は一致しません。

ICMは、プレイヤーのスタック量を入力として受け取り、各順位に入賞する確率を出力する数理モデルです。これらの確率とペイアウト構造に基づいて各スタックの金銭的価値（$EV）を計算し、トーナメントの最適な判断に役立てます。基本的なICMの仕組みについては、別の記事で解説しています。

ICMとチップEVの比較 (ポストフロップ)

まず、「チップを増やすこと」と「賞金を得ること」は、実際どの程度ズレているのでしょうか。以前の記事では、プリフロップのプッシュ／フォールド戦略においてチップEV戦略とICM戦略を比較し、ICM戦略のほうが明確に優れていることを示しました。ただし、これまでの検証はプリフロップに限定されていました。今回、ポストフロップICM解析が可能になったことで、ポストフロップにおけるチップEV戦略とICM戦略の違いを直接比較できるようになりました。

前提条件

比較した3つの戦略

2つの比較検証

それぞれの検証では、チップEVおよびGTO Wizard ICMによるナッシュ均衡でのフロップ戦略を導出し、それをNemesisソルバーでノードロックして、それぞれのEVロスを計測しました。

検証結果

それでは結果を見ていきましょう。各戦略がNemesis ICMに対してどれだけの金銭的価値を失ったかを測定しました。

プリフロップでのアクションやトーナメントフェーズごとに結果を比較すると、ICMの影響がどのタイミングで顕著になるかが明確にわかります。特にバブル時やファイナルテーブルでは、チップEV戦略を採用すると、SRPにおいて毎フロップで参加費の10%以上を失うという明確な差が確認されました。さらに3ベットポットでは、平均して参加費の30%以上を失うケースもあります。

なお、今回ノードロックしたのはフロップ戦略のみであり、Nemesisはターンおよびリバーで完全なプレイを行うと仮定しています。もしターンやリバーも含めて計測していれば、損失はさらに大きくなっていたでしょう。

25%のプレイヤーが残っている段階（15%が入賞）でも、無視できない損失が発生していることが確認されました。これは、ICMを意識した戦略を取ることがトーナメント成功の鍵であることを示しています。

次に、GTO Wizard ICMのバーに注目してください。これは、ほぼ完全なCFRソルバーに対して、私たちのICMアルゴリズムがどれほど高い精度で機能しているかを示しています。評価関数自体は非常に正確で、ICMバリューをほぼ完全に算出しています。GTO Wizard AIは従来と同様に抽象化を用い、1ストリートずつ高速に解く方式を採用していますが、それでも従来のCFRソルバーと比較して圧倒的に短時間で優れた結果を示しました。

CSTE

ICMアルゴリズムの開発中、私たちはトーナメントの種類や進行状況、ポットサイズが異なっても同じ基準で比較できる指標の必要性に気づきました。そこで、Chip-Scaled Tournament Equity（CSTE）という新たな指標を考案しました。

CSTEは、さまざまなフォーマットやトーナメントフェーズで比較可能な正規化値を示します。特に、ICMとチップEVのスポットや、$EVとポットサイズを比較する際に有用です。例えば、ICMバリューに基づく賞金シェアが5%で、トーナメント全体のチップが1000枚ある場合、CSTEは50になります。なお、$EVは「フォールド＝0」を基準としています。

CSTE = 総チップ数 × $EV ÷ 残りの賞金総額

また、同じグラフをCSTE/ポットで正規化して表示することも可能です。これにより、ポットサイズに対してどの程度の搾取余地があるかを相対的に把握できます。

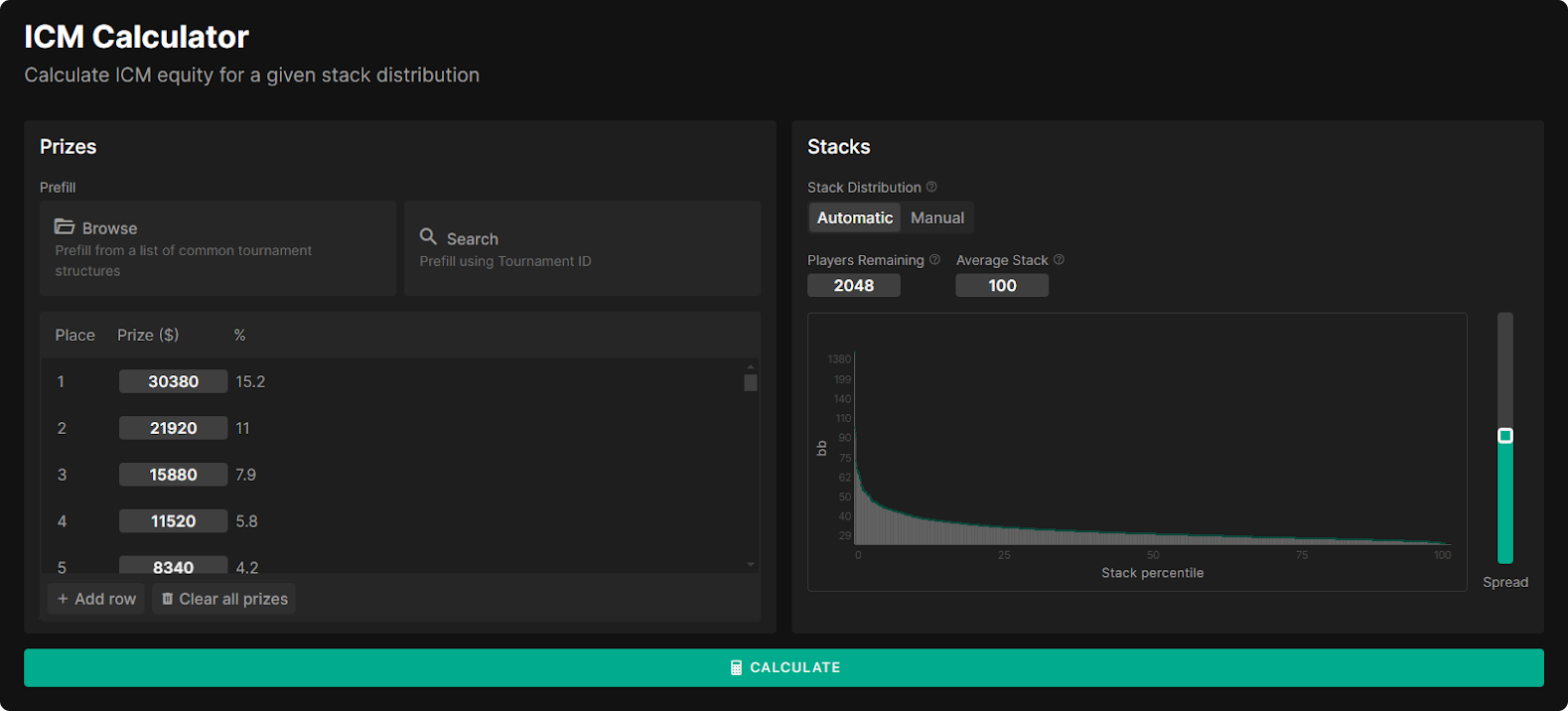
無料で使えるICM計算ツール

GTO Wizardは最大2048人分のスタックに対してICMバリューを計算できる無料ツールを公開しています。プライズストラクチャーとスタックサイズを入力するだけで、ICMバリューに基づいた各スタックのトーナメントエクイティと$EVを算出できます。このICM計算機やGTOソルバーには、作業効率を高める便利な機能が多数備わっています。

主な機能

GTO Wizard ICMの仕組み

GTO Wizardの新しいアルゴリズムは、ICMバリューをこれまでにないほど高精度かつ効率的に計算できるようにしました。これは、以前までは不可能だと考えられていたことです。最大の課題は計算量の膨大さでした。ICMバリューを正確に求めるには、すべてのプレイヤーの順位の組み合わせを考慮する必要がありますが、その列挙はプレイヤー数が増えるにつれて急速に非現実的になります。

30人以上のプレイヤーが参加するトーナメントに対応するためには、すべての順位を一つずつ挙げることなく考慮する方法を見つける必要がありました。最も単純なアプローチはサンプリング法です。可能な順位を確率的に抽出し、その結果に基づいてICMバリューを推定する方法です。この手法により多数のプレイヤーを扱うことは可能ですが、結果はあくまで推定に基づくものであり、精度は十分ではありませんでした。

理論的アプローチのサンプリング法に着想を得て、私たちは高精度かつ高い計算効率を備えた新手法を開発しました。これは完全にアルゴリズム面での革新であり、抽象化・補間・機械学習には依存しません。ICM計算の基礎となる理論数学に基づいており、ICMバリューを高精度に算出します。

その結果、あらゆる形式の入力に対応できる柔軟性と堅牢性を実現しました。この手法の詳細は公開できませんが、従来のICM計算法と比較して、その速度と効率を以下で実証しています。

ICM計算手法の比較

長年にわたり、ICM計算の高速化と効率化を目指して多くの試みが行われてきました。ここでは、代表的な手法と私たちの提案手法を比較します。

ICM計算手法一覧

前提条件

まず、自らのモデルや近似に依存せず、設定内で正確なICMバリューを算出する方法を見つける必要がありました。そこで、1973年に発表された論文「On a Model for Storage and Search」に基づく特別なケースを採用しました。このケースでは、スタックが線形に増加し、賞金が線形に減少します。

このほかにも、基準値が厳密に求められるさまざまな特殊ケースを用いて徹底的に検証を行いました。その結果、最大の相対誤差は**3e-9（0.0000003%）**を超えず、12桁以上の一致を確認しました。

結果

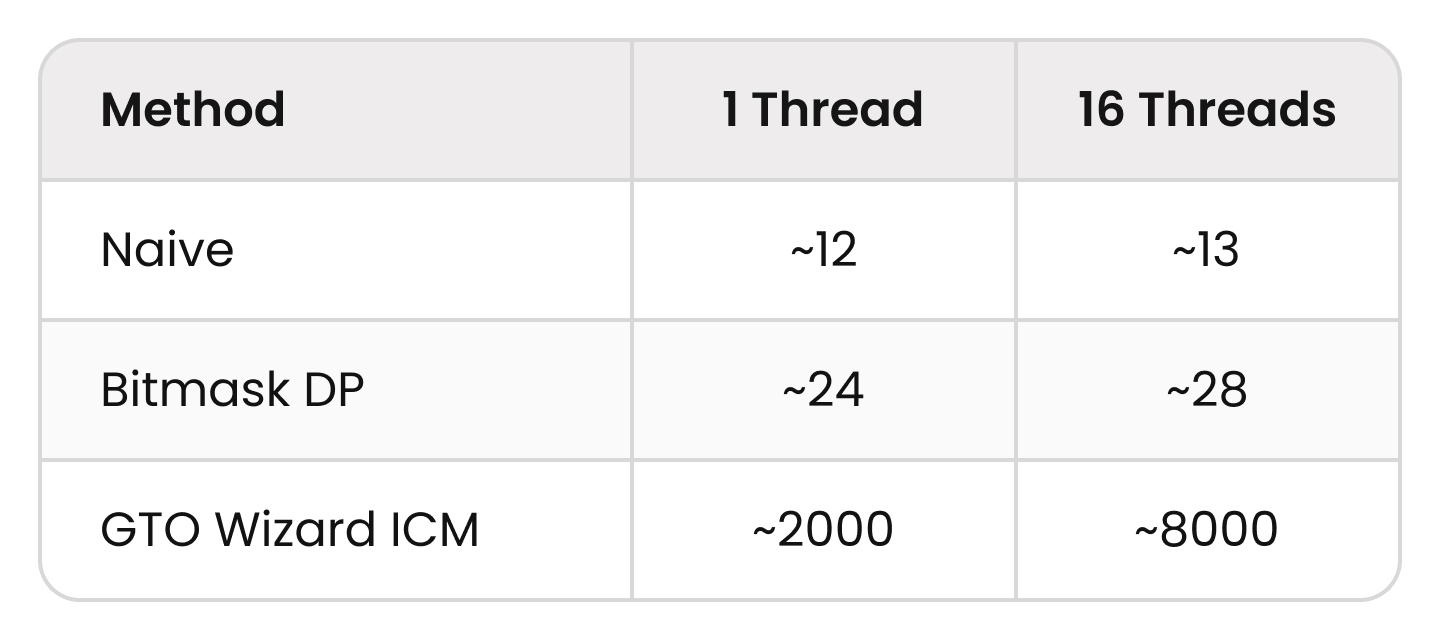
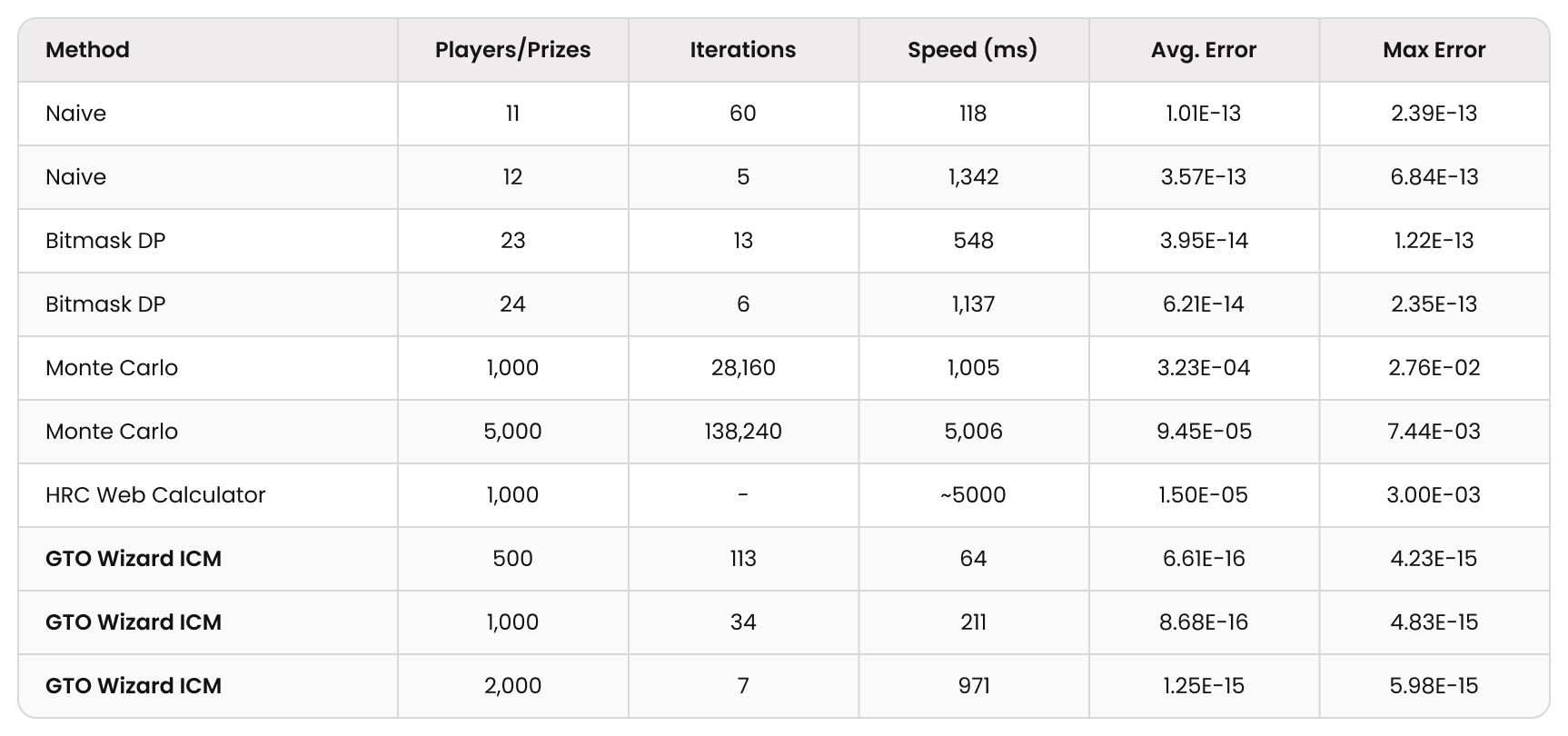
本アルゴリズムは汎用的であり、各テストケース特有の構造に依存しません。さらに、1つのCPUスレッド（Ryzen 7950x）で1秒以内に処理できるプレイヤー数を比較しました。

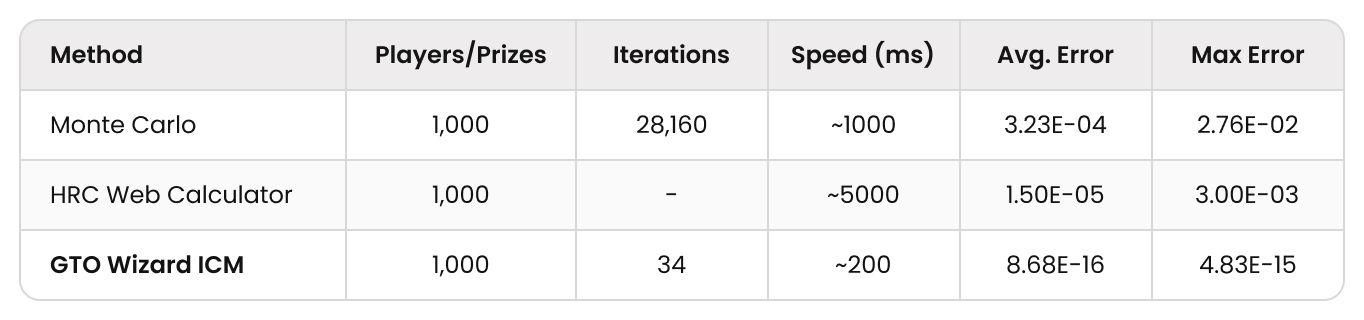
また、近似アルゴリズムであるMonte Carlo法およびHRCとも比較したところ、GTO Wizard ICMは他の手法と比べて非常に高精度で、計算時間も圧倒的に短いことが確認されました。

バウンティのモデル化

近年の多くのトーナメントでは、他のプレイヤーを飛ばすと賞金が得られるバウンティ制（ノックアウト方式）が採用されています。私たちはICM計算モデルを新たに構築しただけでなく、バウンティエクイティを推定するための手法も開発しました。このモデルには、現在のハンドおよび将来のハンドでバウンティを獲得する確率が含まれています。

この詳細な手法については、以下の記事で解説しています。

Bounty Models Explained: Solving Knockout Tournaments

まとめ

MTTの最適戦略を解くことは容易ではありません。チップの価値が一律ではないため、スタックの価値は他のスタックの状況によって変化します。この複雑な問題を解決するため、私たちは次の課題に取り組みました。

その結果、世界で最も強力なトーナメント戦略解析ツールが誕生しました。

本プロジェクトの成功は、多くの仲間たちの貢献によるものです。エンジン開発をリードしたPhilippe Beardsell、新しいICM数式を導き出したWataru Inariba、CSTEを考案したAdam Kellyをはじめ、ポーカー理論の未来を切り拓く情熱と才能にあふれたチーム全員に心から感謝します。