
ブラフはポーカーにおける基本的なスキルであり、相手を欺く要素と戦略的な計算が組み合わさって、ハンドの結果に大きな影響を及ぼします。ブラフの基本を解説した記事や動画は数多くありますが、トリプルバレルブラフの理論に踏み込んだものは少ないのが現状です。
本記事では、ポーカーにおけるマルチストリート・ブラフの数学、特に複数ストリートにわたるブラフの期待値(EV)の計算方法を紹介します。
直感的には、ギャンブルのように見えるブラフを、どのように計算に裏打ちされた戦略へと高めるのか。その数学的基礎を一緒に掘り下げてみましょう。
基本:シングルストリート・ブラフ
まずはシングルストリート(1回のベット)ブラフの基本理論を確認します。
- MDF(Minimum Defense Frequency)を計算する
- 利益的なブラフにするには、相手のフォールド率が1–MDFを上回るようにする
ピュアブラフ(ショーダウンで絶対に勝てないハンドのこと)の期待値も簡単に計算できます。
EV (Bluff) = Fold%(Pot) – Defend%(Bet)
もしこの期待値が正なら、ピュアブラフで利益が出るということです。

しかし、ここで重要なのは次の点です。
もしブラフが(リバー以前に)コールされても、諦める必要はありません。後のストリートで引き続きブラフする選択肢が残っています。
では、その場合の計算はどのようにするのでしょうか?
クイズ
まずは簡単な例を用いて、直感をテストしてみましょう。
あなたはフロップでピュアブラフを持っています。この状況でポットサイズのベットを3回する(トリプルバレル)ことを考えます。相手は必ずフロップとターンでコールします。では、リバーで相手がどれくらいの割合でフォールドすれば、あなたのトリプルバレルの損益分岐点(EVが0)になるでしょうか?
- 50%
- 61%
- 72%
- 83%

C) 72%
(a)を選んだ方もいるのではないでしょうか。リバーでポットサイズのベットをするなら、相手が少なくとも50%(= 1 – MDF)フォールドしてくれればトリプルバレルのピュアブラフが損益分岐点になると考えたかと思います。しかしこの考えでは、フロップとターンでベットした分を考慮していません。リバー単体での損益分岐点ではなく、フロップからリバーに至るまでの損失をも取り戻せるだけの勝率が必要となります。
解説
トリプルバレルを+EVにするには、リバーでフォールドを多くさせなければ、フロップとターンのベット額を取り戻すことができません。リバー単体で損益分岐点を超えるだけでは不十分で、フロップからリバーまでの一連のライン全体で損益分岐点を上回る必要があります。
具体的な計算方法は以下の通りです。
最初のポットを1とし、フロップ、ターン、リバーでポットサイズのベットを順にすると、ベット額はそれぞれ (1, 3, 9) となります。トリプルバレルが最後までコールされれば、合計 (1 + 3 + 9) = 13を失います。相手がリバーでフォールドすれば、(1 + 1 + 3) = 5を獲得します(ポット1+相手がコールしたフロップ1とターン3)。
つまり13をリスクにして5を得る構図なので、13:5 = 13 / (13 + 5) = 72.2%
- 最初のポット = 1
- フォールド時の獲得 = 1(最初のポット) + (1 + 3)(相手のフロップ・ターンのコール分) = 5
- コール時の損失 = 1 + 3 + 9 = 13
- 5を得るために13をリスクにする
- 損益分岐点となるリバーフォールド率 = リスク+リワード=13 / (13 + 5) = 72.2%
よって、リバーで約72%以上フォールドしてくれないと、ポットサイズのトリプルバレルは利益的にはなりません。これより低いフォールド率であれば、フロップで諦める方が期待値的には優れています。
一般的に、複数回のストリートにわたるブラフは、シングルストリートのブラフよりもリスクが増大し、リワードとの比率が悪くなります。
ただし、これは作り話のような極端な例で、普通は相手がフロップとターンを100%コールしてリバーで75%フォールドする、なんてことはありません。次の章で現実的な例を考えてみましょう。
マルチストリート・ブラフの数学
ここからは、もう少し現実的な状況を想定しながら、マルチストリート・ブラフの数学を解説します。
以下の計算は、実際のテーブル上で暗算するためのものではなく、集団の傾向を調べる際などにスプレッドシートを活用して、フォールドしすぎているラインを見つけるためのものです。
また、説明をわかりやすくするため、以下の3つの仮定を置きます。
- 自分がチェックした場合、ブラフは必ず負ける
- ブラフが最後までコールされた場合は必ず負ける
- 相手はコールかフォールドのみを選択する
このとき、取るべき戦略は以下の4つとなります。
- チェック:すぐに諦める。追加でチップを入れないので損失はない。
- ベット → チェック:フロップでベットし、コールされたらターンでは諦める。
- ベット → ベット → チェック:フロップとターンでベットし、コールされたらリバーでは諦める。
- ベット → ベット → ベット:フロップからリバーまで3回ベットする。諦めない。
これら4つの戦略の期待値を計算し、一番高いものを選びます。
戦略(1) チェック
これは即座に諦める戦略なので、EVは0(追加でベットしないため)です。
EV (Check) = 0
戦略(2) ベット → チェック
フロップで1回ベットして、コールされたらターンでは諦める戦略です。これはシングルストリートの計算と同じ要領で求められます。
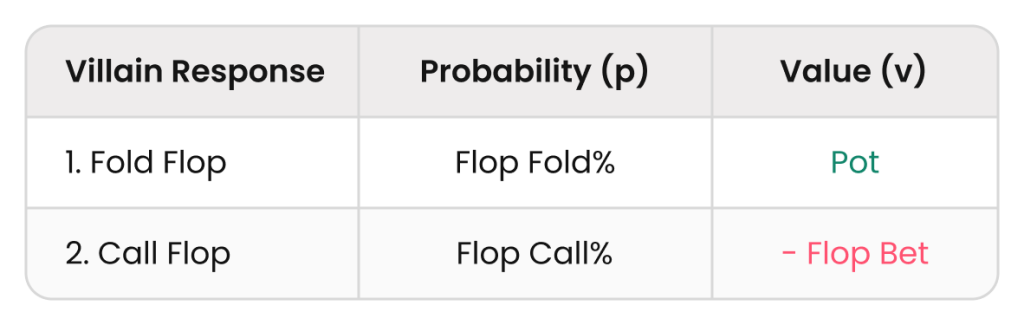
確率 (p) とバリュー (v) を掛け合わせて足すシンプルな式です。
EV (Bet → Check) = p₁v₁ + p₂v₂
具体的には、
EV (Bet → Check) = Flop Fold% (Pot) + Flop Call% (-Flop Bet)
戦略(3) ベット → ベット → チェック
フロップとターンで2回ベットし、コールされたらリバーでは諦める戦略です。下記の3パターンとなります。
- フロップでフォールドさせる
- フロップはコールされるが、ターンでフォールドさえる
- フロップとターン両方をコールされ、ベット2回分を失う

期待値は以下のように計算できます。
EV (Bet → Bet → Check) = p₁v₁ + p₂v₂ + p₃v₃
より詳しく表すと、
EV (Bet → Bet → Check) = (Flop Fold%) (Pot) + (Flop Call% Turn Fold%) (Pot + Flop Bet) + (Flop Call% Turn Call%) (-Flop Bet – Turn Bet)
戦略(4) ベット → ベット → ベット
最後に、フロップからリバーまで3回ベットする戦略を考えます。ここでは4パターンの結果があります。

EV (Bet → Bet → Bet) = p₁v₁ + p₂v₂ + p₃v₃ + p₄v₄
スプレッドシートを使って計算する
見てもわかる通り、数式は長くなりますが、複雑というよりは単純に面倒なだけです。こうした作業こそスプレッドシートが得意な領域です。こちらから無料のスプレッドシートをご利用ください。
使い方は簡単で、ストリートごとのベットサイズやフォールド率を入力するだけです。上記の仮定に基づく計算により、それぞれの戦略のEVを自動的に出してくれます。
例
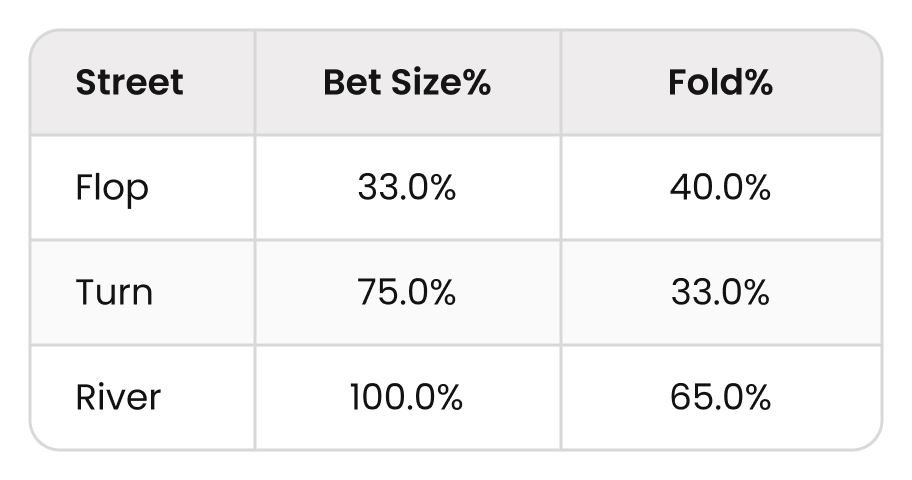
フロップでピュアブラフを持っているとします。また、対戦相手は次のような傾向を持っています。フロップではフォールドしすぎる(over-fold)、ターンでは少しコールが広い(over-defend)リバーでは怖がって降りがち(plays scared money)
ここで、先ほどのようにベットサイズとフォールド率を入力します。
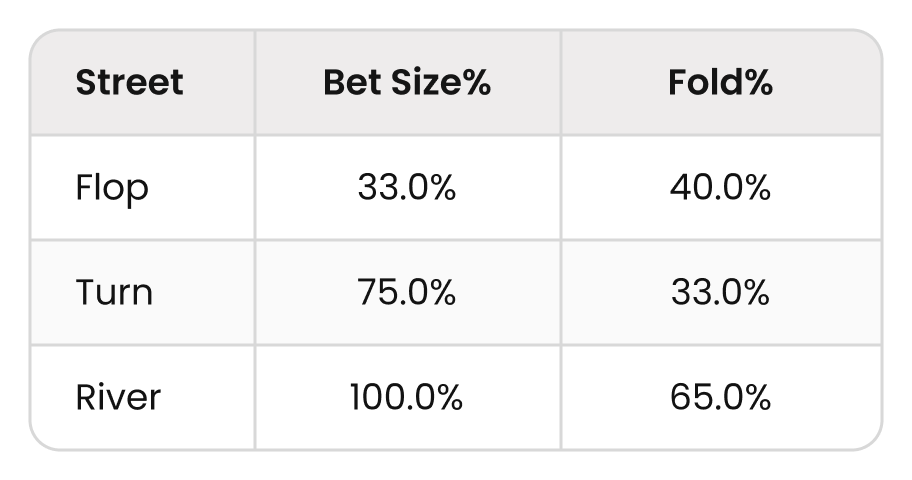
最初のステップは、ベットサイズを%からチップに変換することです。ポットが大きくなるにつれてリスクも増えるため、ベットサイズを常にパーセンテージのまま扱うと計算がややこしくなります。そこで、最初のポットを1チップとして計算します。
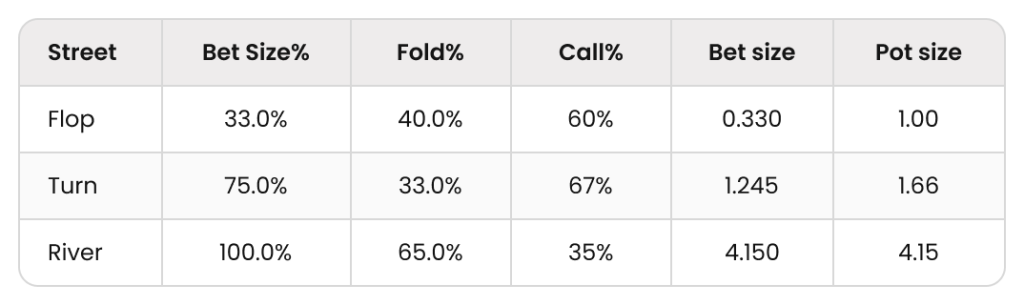
ステップ2は、各戦略のEVを計算します。
戦略(1) チェック
すぐに諦める
EV = 0
戦略(2) ベット → チェック
フロップで1回ベットし、コールされたら諦める。
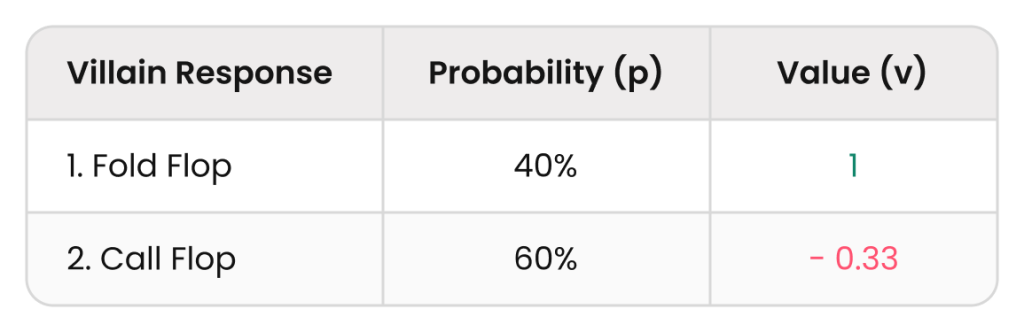
EV (Bet → Check) = p₁v₁ + p₂v₂ = 0.4 – 0.2 = 0.2
つまり、0.2のプラスEVになります。
戦略(3) ベット → ベット → チェック
フロップ・ターンでベットし、コールされたらリバーで諦める。
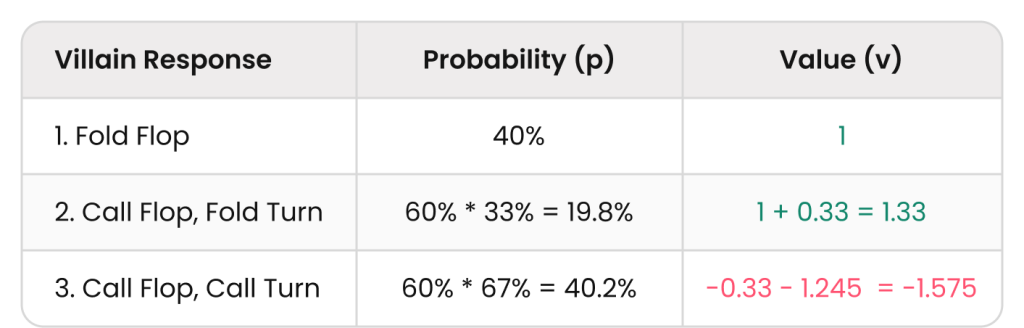
EV (Bet → Bet → Check) = p₁v₁ + p₂v₂ + p₃v₃ = 0.4 + 0.263 – 0.633 = 0.03
結果は0.03のプラスEVです。
しかし、戦略(2)と比べてEVが低くなっています。これは、ターンで相手がコールしすぎるため、フロップで得たフォールドエクイティの大部分を失ったからです。フロップでフォールドエクイティの大部分(0.4)を得たものの、ターンバレルで0.37失っています。
戦略(4) ベット → ベット → ベット
リバーまで3回ベットし続け、諦めない場合。
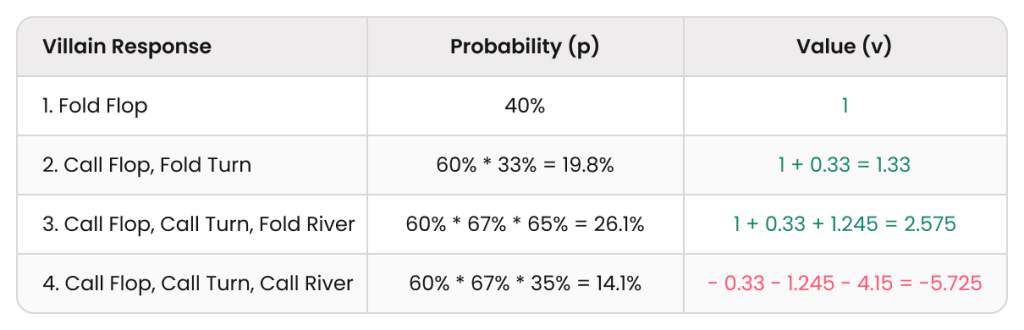
EV (Bet → Bet → Bet) = p₁v₁ + p₂v₂ + p₃v₃ + p₄v₄ = 0.4 + 0.263 + 0.672 – 0.807 = 0.528
結果は0.53のプラスEVとなり、今回の4つの戦略の中では最も高いEVとなっています。
ターンバレル自体は不採算でしたが、リバーでさらにブラフを続けることで、損失以上に利益を出すことができています。
ステップ3は、戦略を比較します。
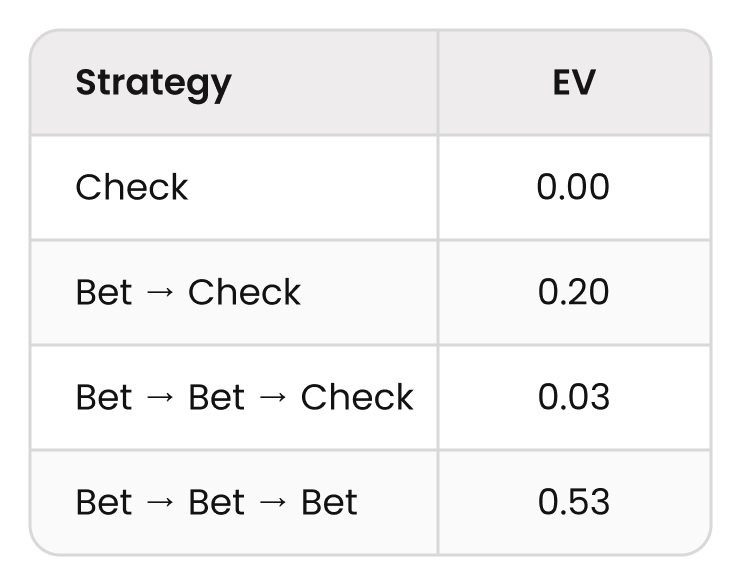
このように計算されたEV(ここでは最初のポットを1とした場合に対する値)を比較し、最も高いEVを示す戦略を選日ます。もし最初のポットが10であれば、ここで得られた数値をすべて10倍にしてください。
ベット → チェック → ベットはどうなのか?
これまで、チェックは「諦める」という前提でした。しかし、現実には、ターンでチェックしてもリバーでは再度ベットできる可能性があります。
今回の例では、相手はターンでコールしすぎるけど、リバーでは降りすぎる。ではターンをチェックして、リバーでベットするのはどうか?
という発想が浮かびます。そこで、次のような新たな戦略(5)を追加して考えてみましょう。
戦略(5) ベット → チェック → ベット
- ターンでチェックしたら、相手が50%の確率でベットしてくると仮定し、こちらはそのベットにフォールドするとします(相手はバリュー重視のレンジでベットしてくる、と想定)。
- ターンでチェックバックされた場合(相手がベットしてこなかった場合)、リバーでポットサイズに対して1.66チップをベットし(約ポットベット)、75%のフォールド率を想定するとしましょう。

EV (Bet → Check → Bet) = p₁v₁ + p₂v₂ + p₃v₃ + p₄v₄ = 0.4 – 0.099 + 0.299 – 0.149 = 0.451
結果として、0.45のプラスEVが得られます。一見良さそうに見えますが、先ほどのトリプルバレル(戦略(4))のほうが0.53と、さらに高いEVを得ています。
まとめ
多くのポーカー理論は一つのストリートのみで計算をしています。しかし、実際に複数ストリートにわたるブラフを考える場合、ストリート1つだけの計算だけでは不十分です。たとえば「多くの人はリバーで降りすぎだから、そこを狙う」とよく言われますが、それだけでは、フロップやターンでの不採算を補えるかどうかがわかりません。複数ストリート全体のEVを把握することが重要です。
マルチストリートにおけるブラフのEV計算は決して難しくありませんが、手作業では面倒でしょう。したがって、実戦での大量のデータを分析する場合は、スプレッドシートなどの計算ツールを使って多くの場面を効率よく検証してください。
もちろん、テーブル上でいきなり複雑な計算をするのは現実的ではありませんが、テーブル外でこうした分析を行っておくと、「いつ」「どんな相手に」「どんなラインを取るか」といった判断がより的確になります。
最後にいくつかのポイントをまとめます
- マルチストリートでのブラフはシングルストリートよりもリスクリワード比が悪くなりやすい。
ストリートを経るごとにポットが大きくなり、リスクが増大します。 - リバーでのブラフが単体でプラスEVでも、フロップやターンでのマイナスEVを補えない可能性がある。したがって、リバーのEVだけでなくフロップ→ターン→リバーまで一貫したラインのEVを考慮する必要があります。
- EV計算をする際は、すべての戦略とそれらのあらゆる結果を分解して考えてください。複雑な数式を一度にまとめようとするよりも、表形式で結果を整理するとわかりやすくなります。
- ライブゲームのテーブル上では即座に詳細な計算を行うのは難しい。こうしたマルチストリート・ブラフのEV分析は、基本的にテーブル外で行い、エクスプロイト(相手の弱点を突く)戦略に反映させましょう。
- 「一見もっともらしいライン」が必ずしも「最も利益が高いライン」ではないこともある。直感や常識に捉われすぎず、きちんとEVを計算してみることが大切です。



