ICMはポーカーにおけるトーナメント戦略を理解する上で最も重要な公式の一つです。この概念は1987年にM.Malmuthによって考案されましたが、その概念を正確に使えるようになるまで35年近くかかりました…
ICMはトーナメントのスタックを評価するのに効果的な概念ですが、最近まで、多くのプレイヤーが残っている大規模なMTTを計算するのはほぼ不可能でした。そのため、多くのプレイヤーが残っている場合、全てのプレイヤーはチップEVモデルを使ってトーナメントにおけるスタックの価値を判断していました。近年のポーカーの発展により、数百人、数千人のプレイヤーが残っていてもICM を計算できるようになりました。
しかし、まだ重要な疑問が残っています。トーナメントにおいてICMが重要な意味を持つようになるのはどの時点からでしょうか?どのタイミングでICMソリューションに切り替えるべきでしょうか?その答えを見つけるため、Holdem Resources Calculatorの創設者であるHelmuth氏と共同で、以下のような一連の実験を行いました。
復習 ー ICMとは
ICMは、トーナメントでのスタックをチップからドルに変換する数式のことです。ICMは、スタックサイズでプレイヤーがそれぞれの順位(1位、2位など)でフィニッシュする頻度を決め、その順位のペイアウトに基づいてトーナメントエクイティを割り当てます。トーナメントエクイティとは、ペイアウトストラクチャーやポジション、スタックサイズを考慮した上で、プライズプールの分配を予想したものです。
ICMの計算方法について詳しく知りたい方は、こちらの記事をご覧ください。直感的にICMを理解したい場合はこちらの動画をご覧ください。
ICMとチップEV
この2つは同じではありません。ICMでは、より多くのお金を獲得するためにチップを犠牲にすることが多々あります。この概念は「リスクプレミアム」と呼ばれます。MTTでは、長く生き残るためにギリギリの局面を避けることが正しいプレイとなることが多々あります。そしてチップを失うことは同じ額のチップを得ることよりもダメージが大きくなります。逆にチップリーダーは、自分よりスタックの少ない相手がより慎重にプレイすることを期待できるため、アグレッシブにプレイします。こういったリスクを回避するような動きは、チップEV戦略では起こり得ません。チップEV戦略はそういった要素を恐れずにチップを最大化することだけを目指しています。
ドルのためにチップを犠牲にするのは果たして正しいプレイと言えるのでしょうか?
さらに掘り下げていきます。
実験方法
この実験の目的は、どの時点でICMがMTTにおいて重要な要素になるかを見つけることです。どの時点でチップEVモデルからICMモデルに切り替えるべきかを知るために一連の実験を行いました。戦略の構成を変えてトーナメントをいくつかシミュレーションして、どの戦略の構成が最も利益的かを調べました。
戦略構成
- ICM 100% (ICMのみ)
- cEV 25% -> ICM 75
- cEV 50% -> ICM 50%
- cEV 62.5% -> ICM 37.5%
- cEV 75% -> ICM 25
- cEV 95.5% -> ICM-FT (ファイナルテーブルのみ)
例えばcEV 25% -> ICM 75%の場合、25%のプレイヤーが脱落するまでチップEV戦略を使い、残りのプレイヤーが75%になった時にICM戦略に切り替えます。各トーナメントで同じ数の戦略構成を試してみます。それぞれの結果を表にまとめて、どの時点でICMに切り替えると結果に大きな違いが生まれるのかを調べます。
実験1– 参加者200人のフリーズアウト
条件
- 参加者200人のフリーズアウト
- 上位15%がITM
- オールインかフォールドのみ
- BB = 平均スタックの1/7
- すべてのプレイヤーはお互いの戦略を知っていて、お互いにエクスプロイトし合う。
- サンプル数 = 500,000回
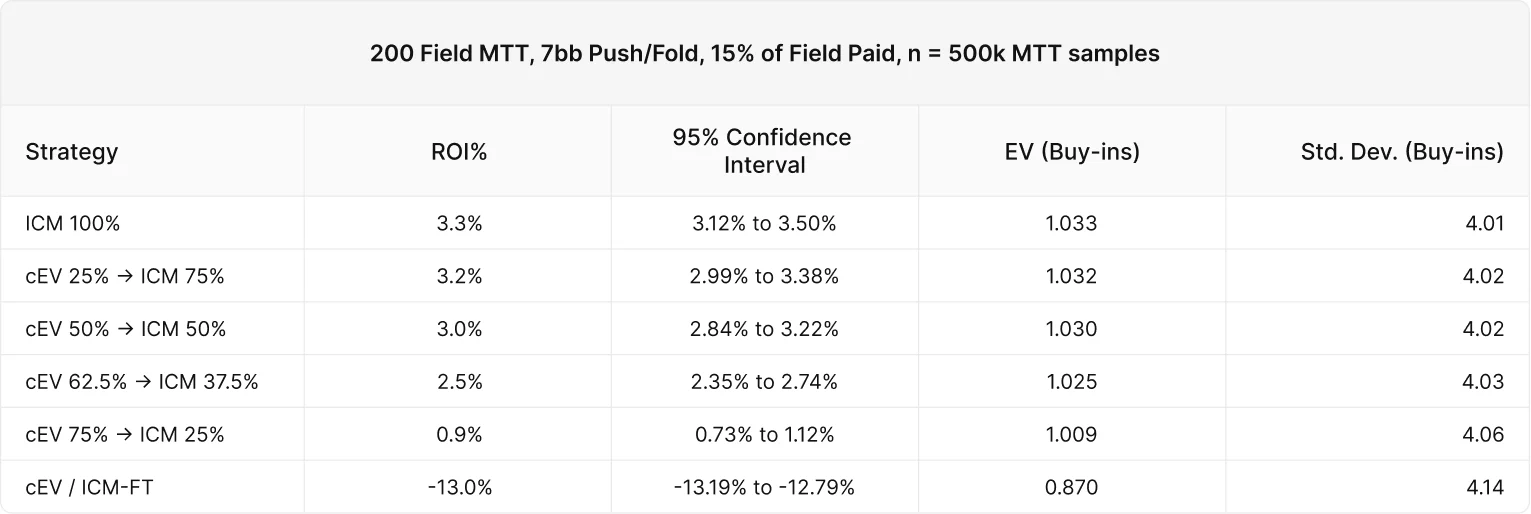
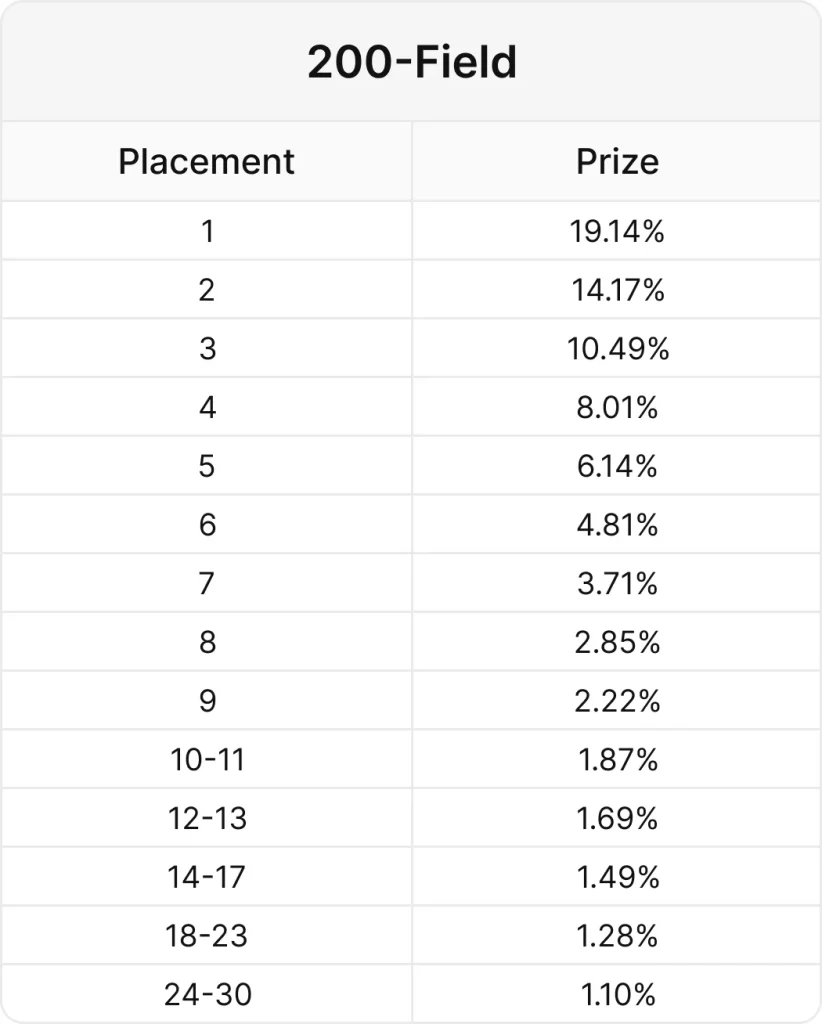
200人が参加するフリーズアウトの例をみてみましょう。これはオールインとフォールドしかアクションがないトーナメントで、BBは平均スタックの1/7に調整され、平均スタックは常に7BBとなります。これはプレイヤーが飛ぶ度に調整されます。オールインかフォールドしかないので、プリフロップの戦略のみをシミュレーションします。すべてのプレイヤーはお互いの戦略を知っており、お互いにエクスプロイトし合います。
結果
次のグラフは、各戦略構成のROIを示しています。ご覧の通り、ICMに早く切り替えたプレーヤーの方が平均勝率が高くなっています。
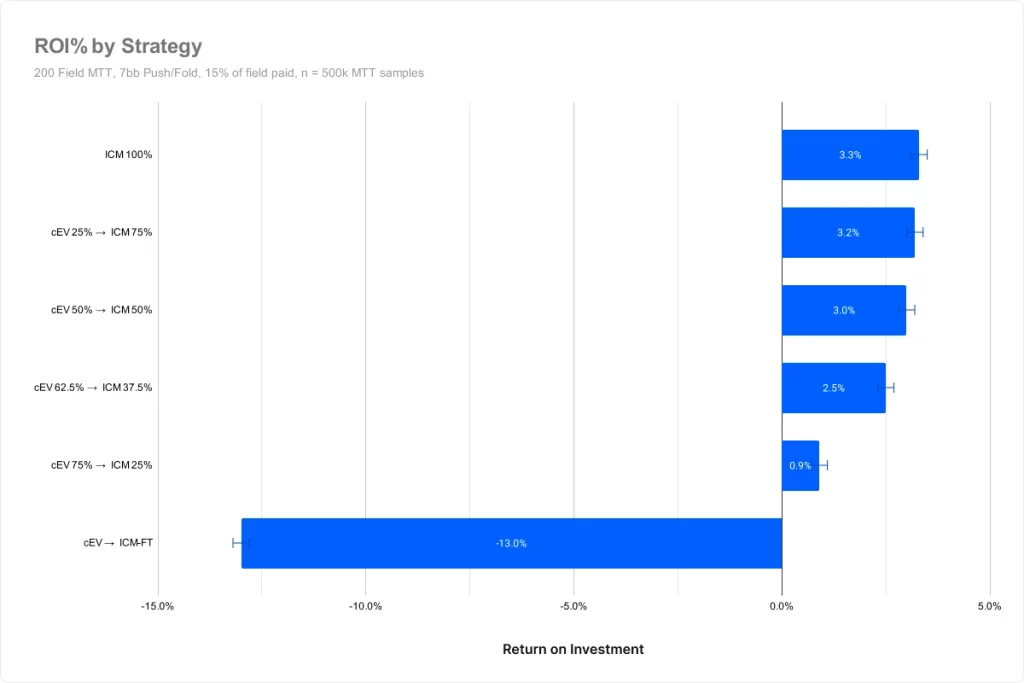
参加者の残りが50%から37.5%の間で、グラフがわずかに減っています。この損失は統計的有意性を超えており、分散のせいではないことが分かります。
これはICMがバブルよりかなり前から重要な要素であることを示しており、予想外の結果となりました。参加者の上位15%がプライズを得られるため、バブルは残りプレイヤーの15%で発生します。しかし、cEV 75%/ICM 25%は、バブルのかなり前にICMに切り替えたにもかかわらず、大きな損失を出しています。
最下位、cEV 95.5%/ICM 4.5%は平均してバイインの13%を失っています。この構成はチップEVを使い、チップを最大化します。そしてファイナルテーブルでのみICMに切り替えます。
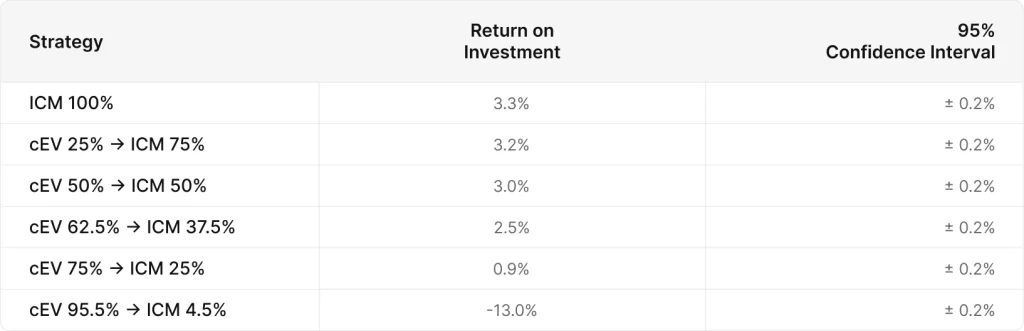
順位表
この差は一体何が要因なのでしょうか。以下のグラフは、それぞれの戦略構成のITMの割合を示したものです。
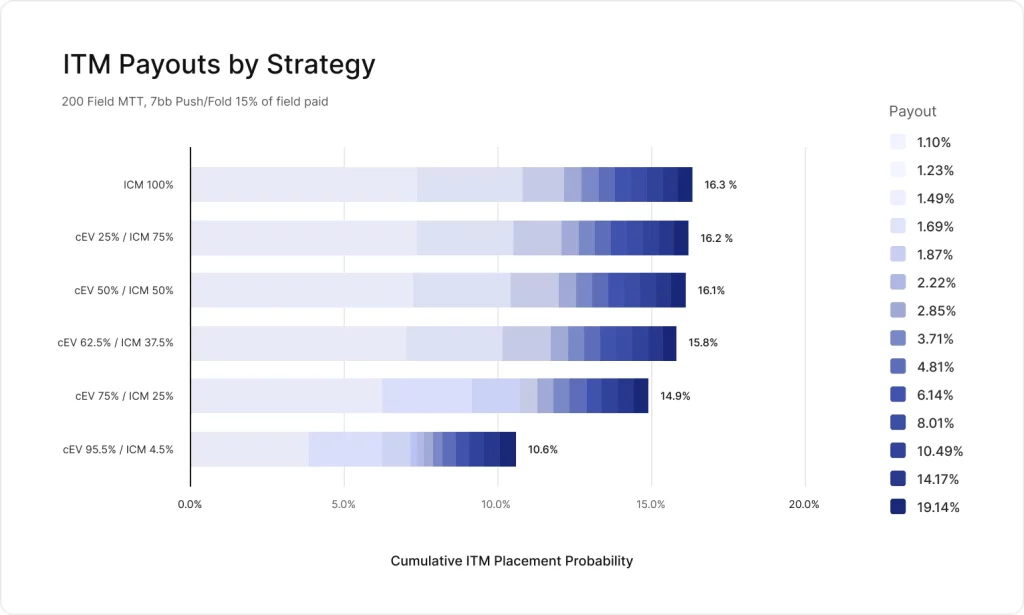
より早くICMに切り替えた戦略は、より頻繁にITMしていることがわかります。これがICMが全体的にROIが高い理由です。
さらに細分化します。次のグラフは、各戦略がそれぞれの順位を達成する頻度を示しています。
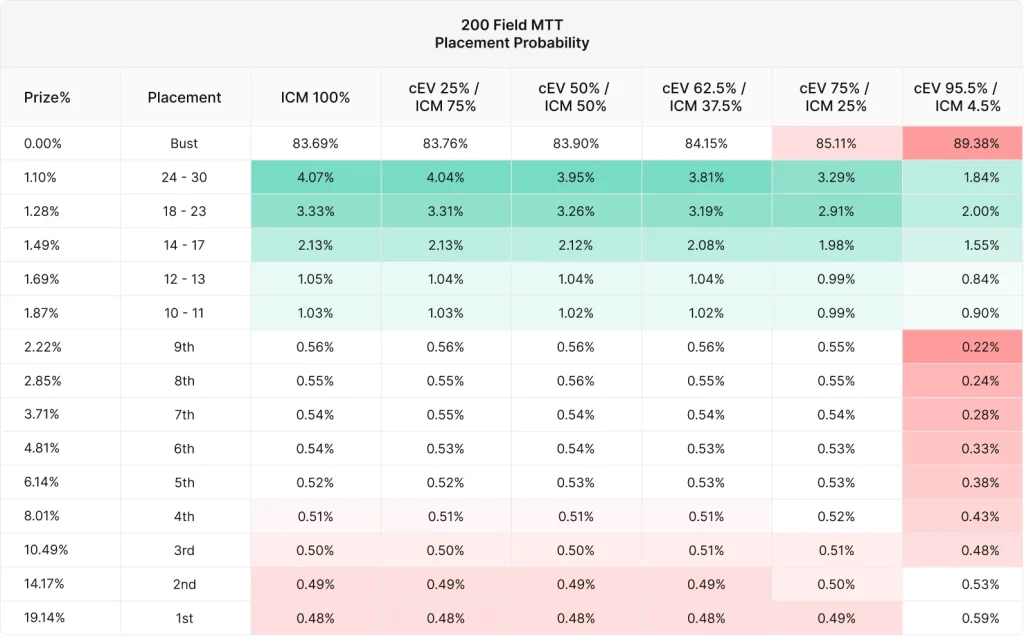
右側のcEV95.5%/ICM4.5%はバストの頻度が高く、ITMの頻度が低いことがわかります。この戦略構成はファイナルテーブルまでチップEVでプレイしていたことを思い出してください。
しかし、cEV戦略は他の戦略よりも1位になる確率が高くなります。これはある意味あたり前です。ICMや他のMTTエクイティモデルは、1位になる確率はトーナメントにおけるチップの割合に等しいことを前提にしています。そのため、ITMを犠牲にしてチップを最大まで獲得するcEV戦略は、1位になる確率が最も高くなるのです。
標準的な順位に対する割合の変化
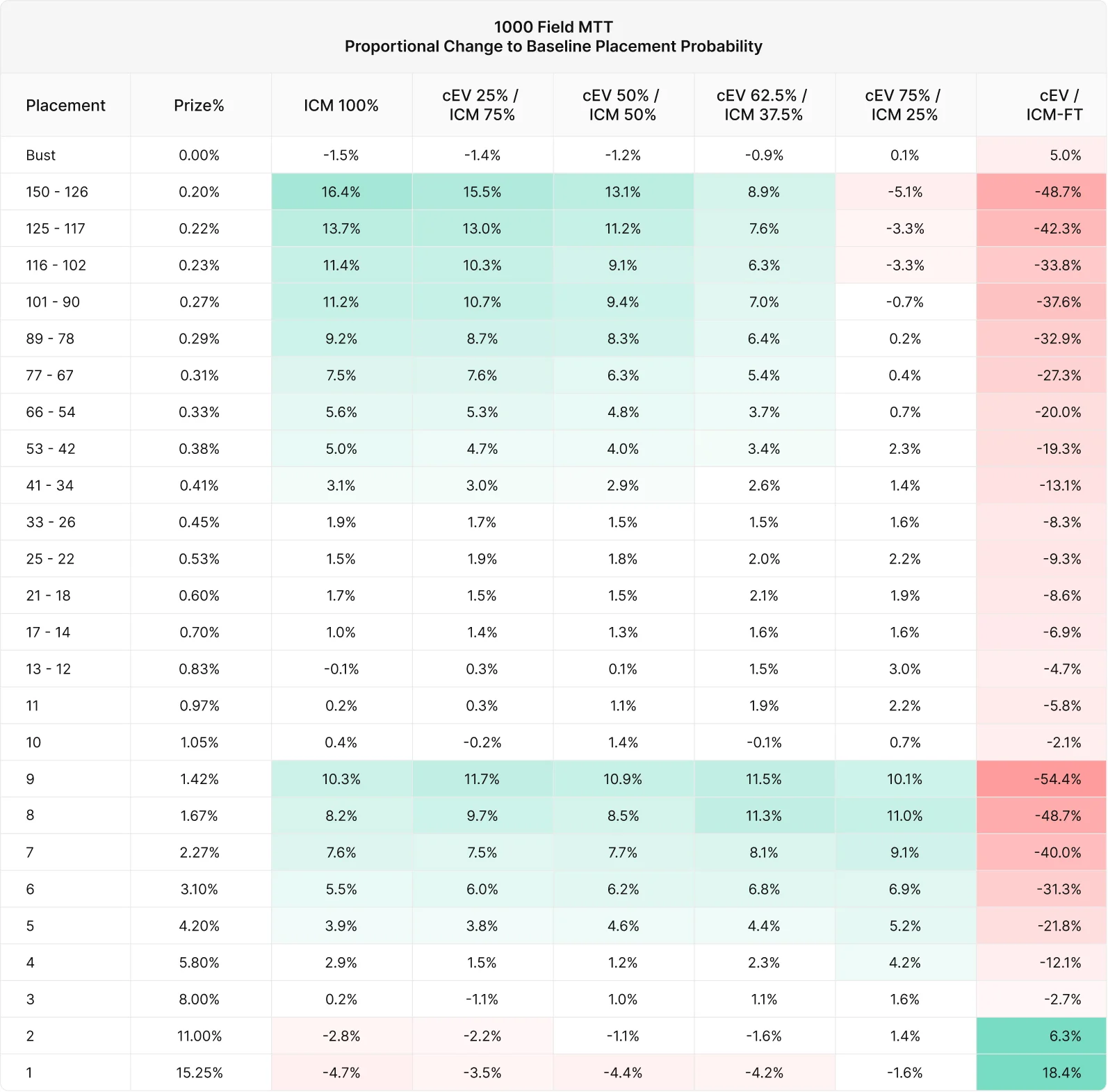
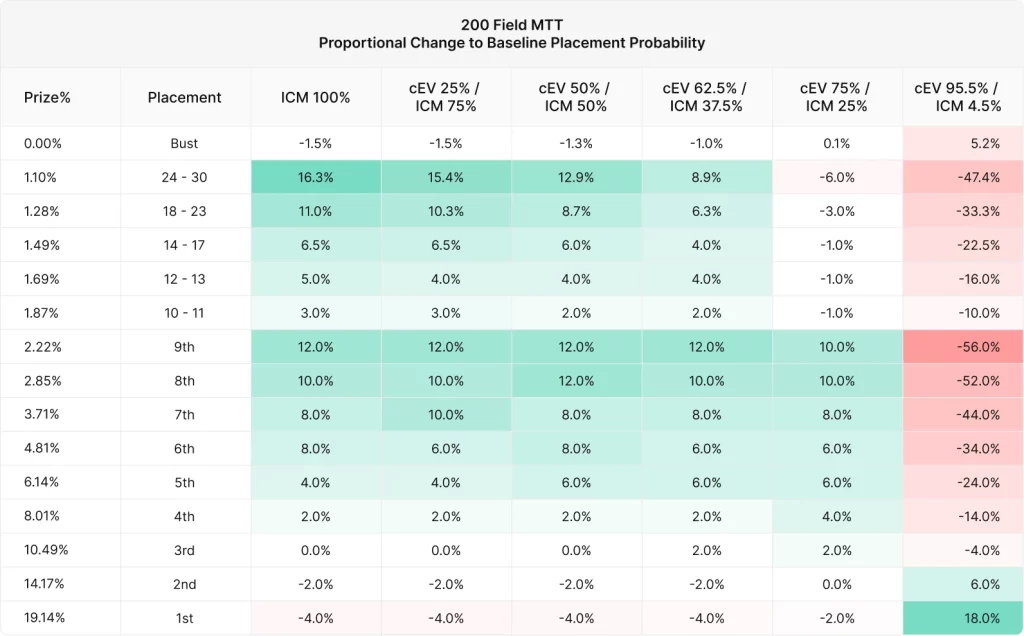
それぞれの順位を取る確率を「標準的な順位」と比較することができます。以下のグラフは、標準的な順位を取る確率に対する割合の変化を示しています。
- 標準的な確率= ランダムに選ばれた場合の各プレイヤーの順位の頻度
- 比率の変化 = 実際の順位の確率 / 標準的な順位の確率 – 1
つまり、cEV 95.5% / ICM 4.5%戦略はランダムな場合と比較して1位になる確率が18%高いですが、バストする確率も5.2%高いことが分かります。
EV
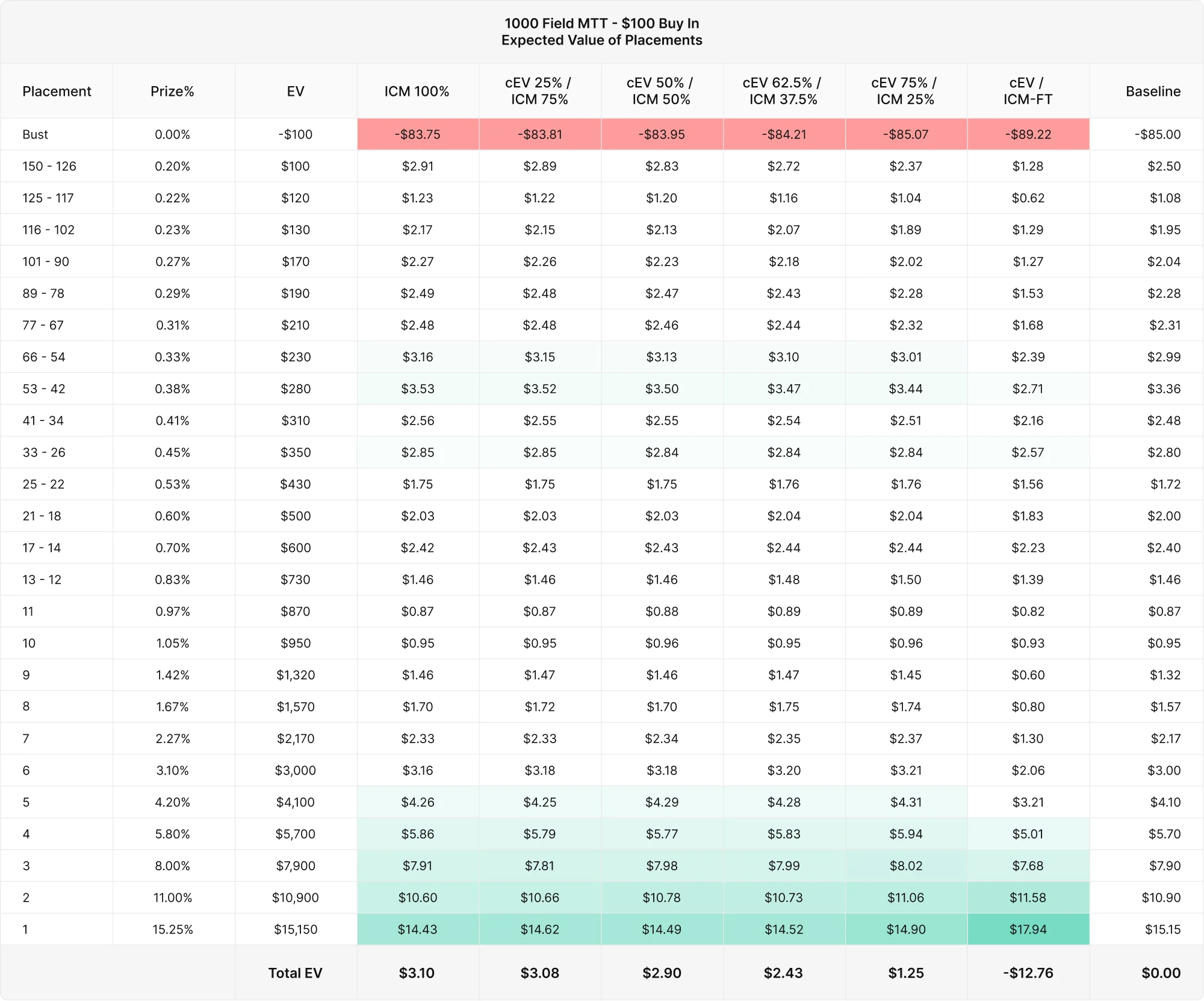
ここで最も重要になるのはEVです。バイインは100ドルとし、それぞれの順位の頻度にそのプライズのEVを掛け、戦略の損得を計算します。このトーナメントのプライズプールは$20,000です。
EV = プライズ率 × プライズプール × 順位の頻度 – 100ドルバイイン
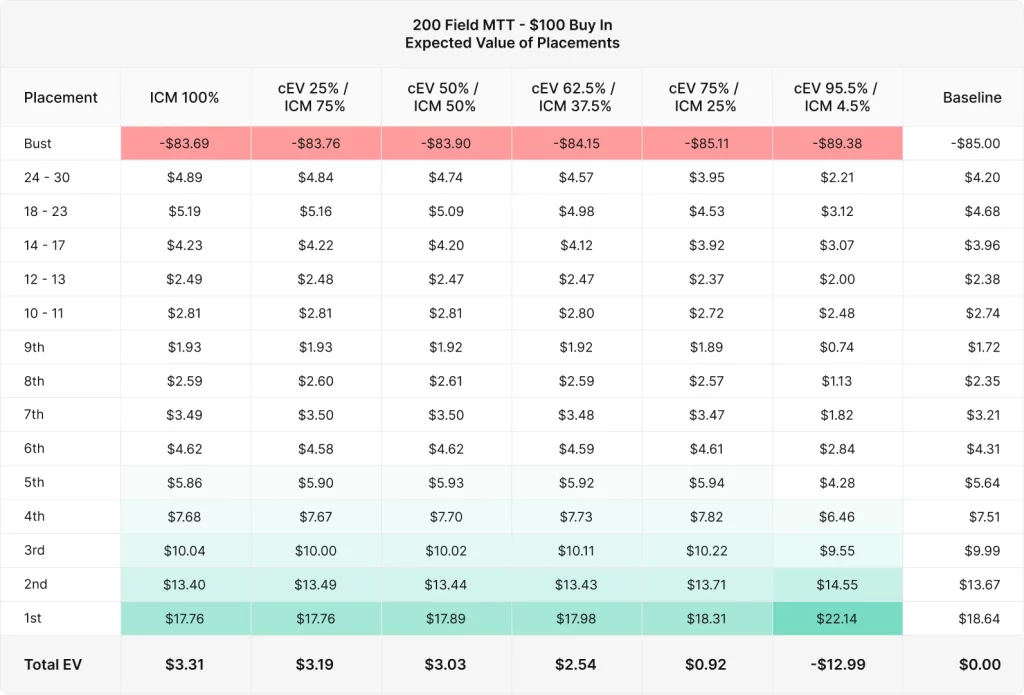
トーナメント内で、それぞれの順位でどれだけのプライズが得られるかは面白い結果となっています。
この表は、標準的な順位のEVの変化をわかりやすく表しています。ICM100%からICM37.5%までの戦略では、2位と1位を除くすべての順位でEVを獲得しています。これはICMの特定を強く表しています。つまり、MTTでは生き残ることこそ全てということです。一方、ICM25%以下の戦略は、バブルでのEVを犠牲にする代わりに、上位の順位でのEVが高くなっています。
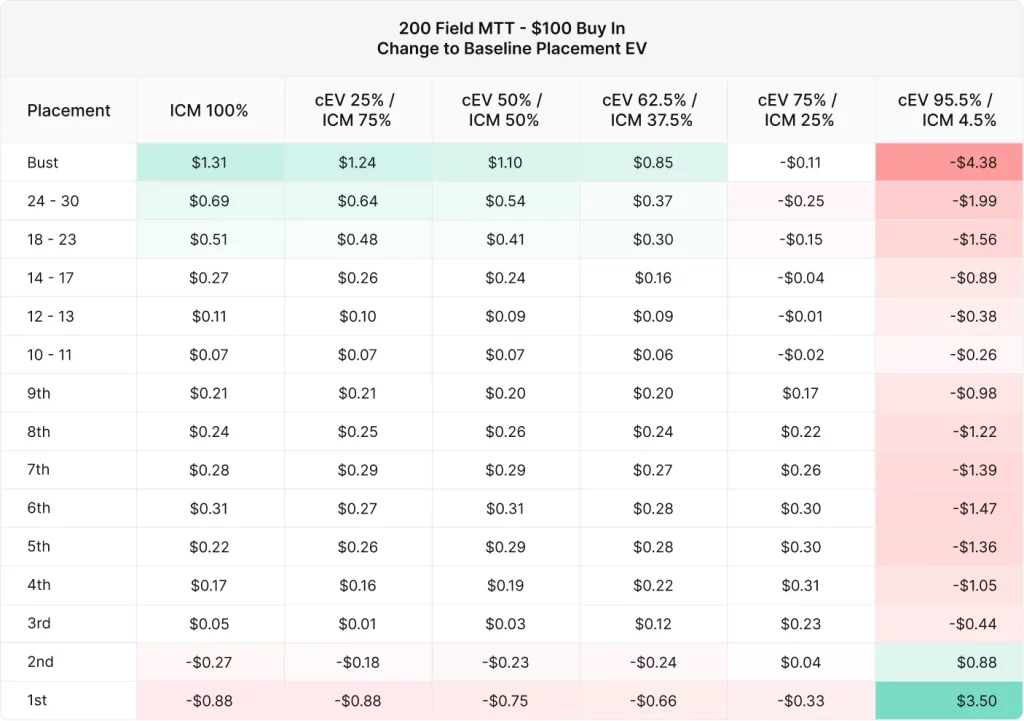
最後に、戦略別の順位のEVをグラフにします。
戦略ごとのEVの曲線はどれも似通っていますが、1つだけ大きな外れ値があります。 cEV 95.5% / ICM 4.5%戦略です。
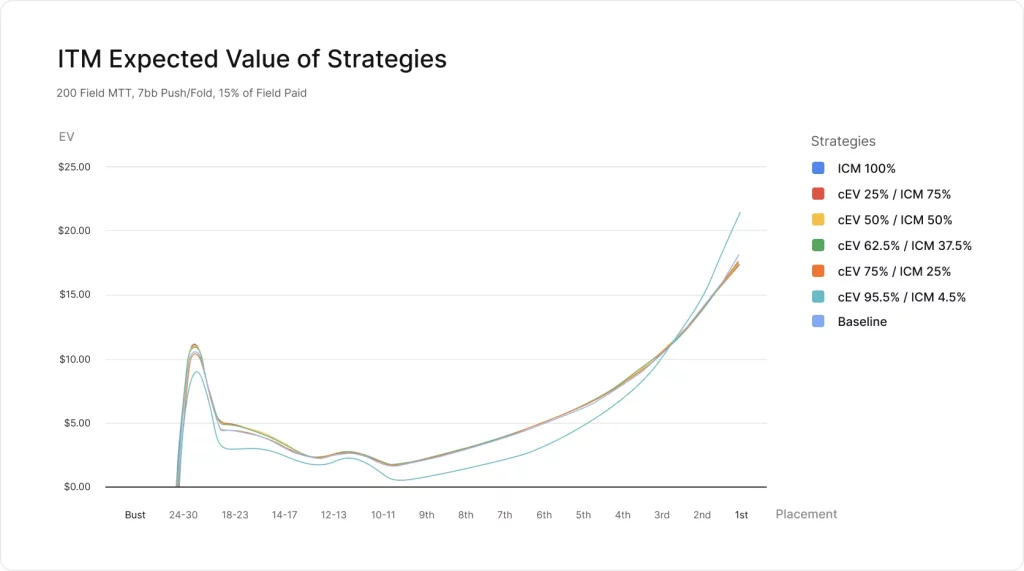
このグラフから、cEV戦略はチップを最大にして1位を狙う代わりに多くのドルを犠牲にしていると言えます。他の戦略の違いが分かりにくくなるほど、このEVの曲線は他の戦略と大きく乖離しています。
実験2 – 参加者1000人のフリーズアウト
実験を繰り返すことは、結果の有益性に確証を持つための手法として非常に有用です。実験を繰り返し、変数を外していくことは、科学的なアプローチにおいて非常に重要です。
今回の実験では、より大規模に先ほどの方法を繰り返します。結果にはプライズストラクチャーや参加人数の影響で外れ値が含まれているかもしれないため、注意しながら進めていきます。先ほどと同じ条件で、今回は参加者1000人のフリーズアウトをシュミレーションします。
条件
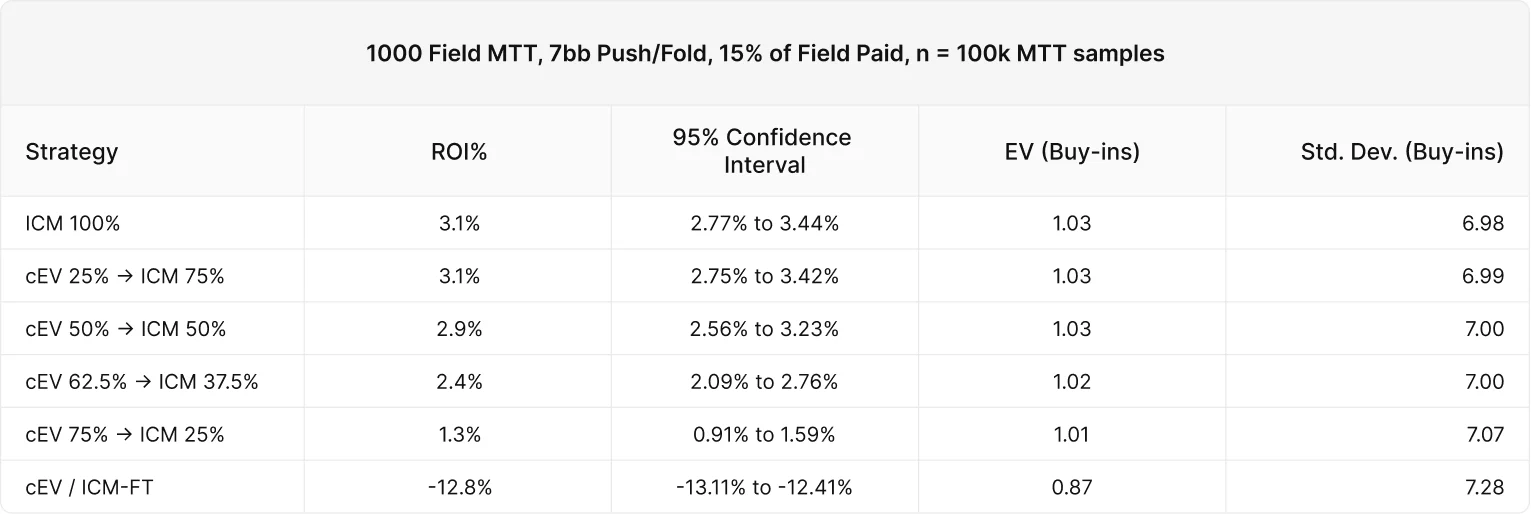
先ほどと同じ条件で、今回は参加者1000人のフリーズアウトをシュミレーションします。
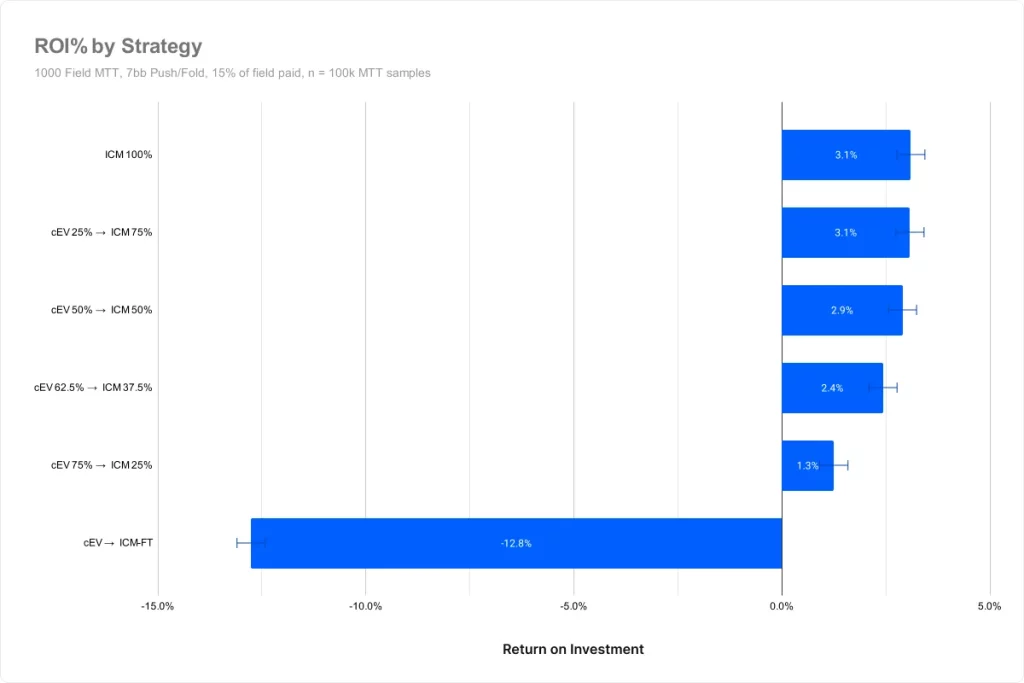
- 参加者1000人のフリーズアウト
- フィールドの15%がITM
- オールインかフォールドのみ
- BB = 平均スタックの1/7
- 6つの戦略構成
- すべてのプレイヤーはお互いの戦略を知っていて、お互いにエクスプロイトし合う。
- サンプル数 = 100,000回
結果
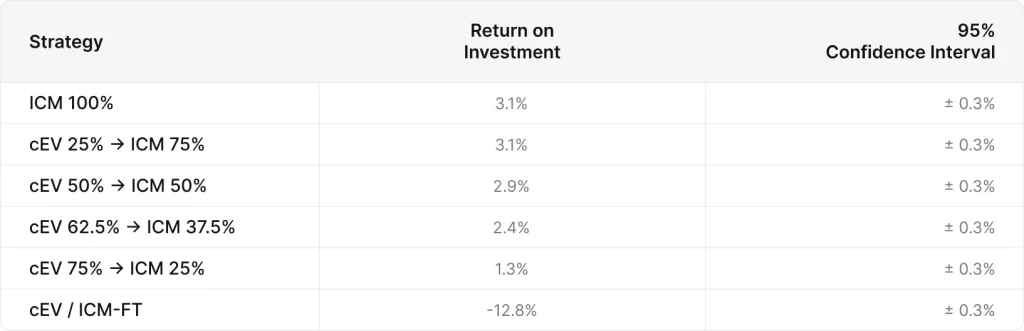
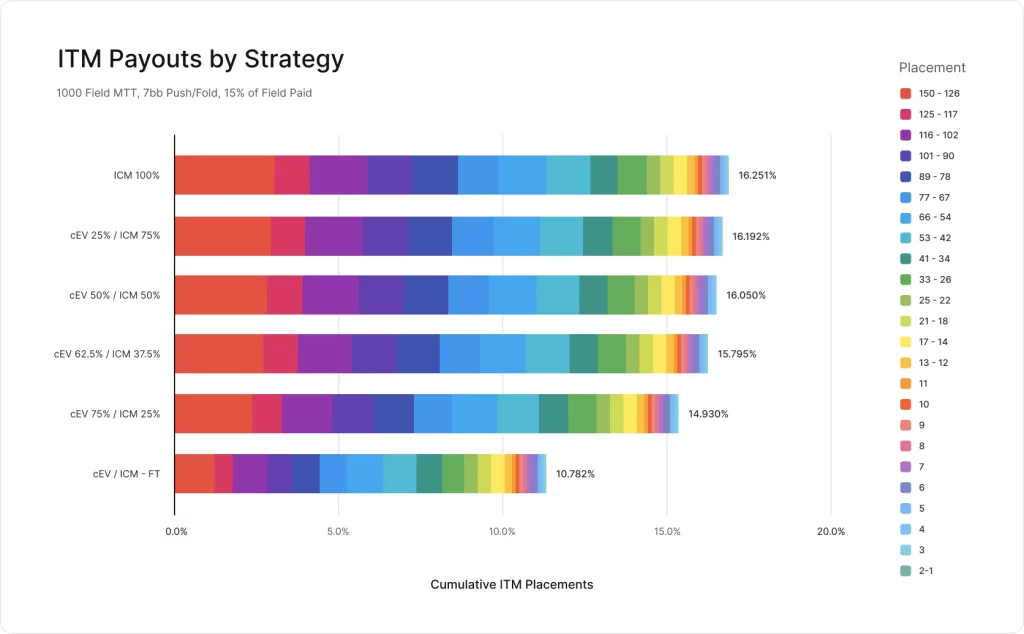
前回と同様に、ICMに早く切り替えた戦略の方が平均して良い結果が得られています。ROIが下がり始めるのは、cEV 50% / ICM 50%とcEV 62.5% / ICM 37.5%の間のどこかだと分かりました。
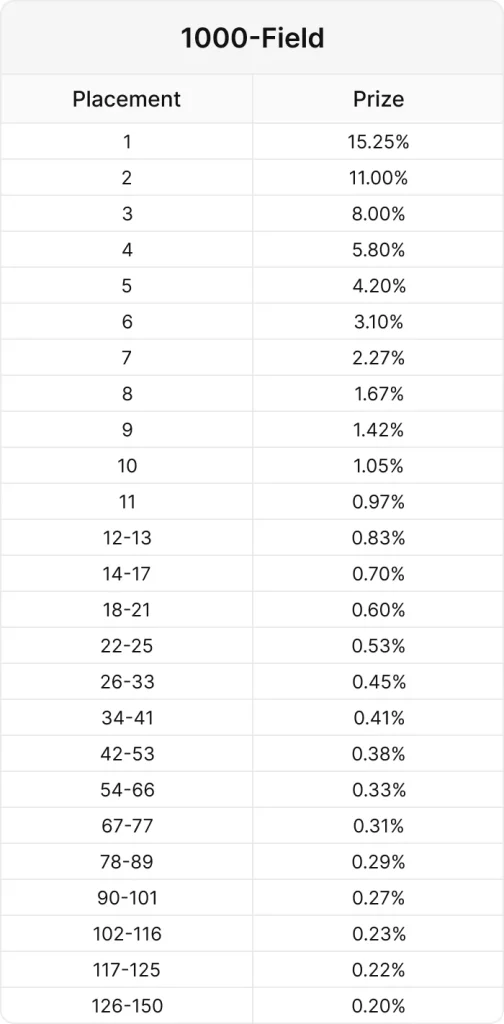
どちらの実験でも、ICMは参加者の残りが50%から37%の区間において統計的に有意な影響を与え、15%よりも多くITMしています。信頼区間により、純粋なICMがICM50%より優れていると主張することはできませんが、一般的な傾向は先ほどの結果と一致しているようです。
順位表
前回と同様に、ICMに早く切り替えたプレイヤーは、全体的にITMしやすくなります。
EV
標準的な順位に対するEVの変化
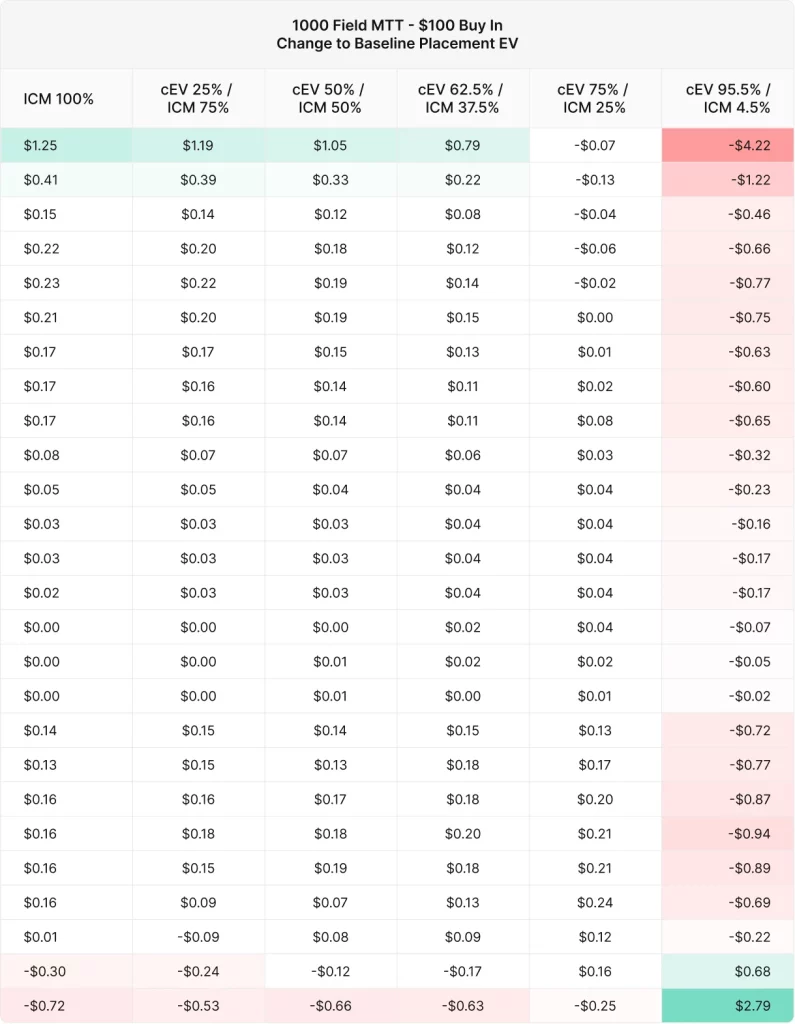
200人での実験と同様に、早くICMに切り替えたプレイヤーはITMする頻度が高い代わりに、最上位の順位付近のEVは若干低くなっています。逆に、ICMに切り替えるのが遅いプレイヤーは、より深いスタックを築き上げて、より多くのリスクを負う傾向があり、その結果、最も高い順位で高いEVを獲得できている反面、ITMの頻度は低くなっています。
この表は、標準的な順位に対するEVの変化を表しています。
実験3 – 追加の戦略
このシミュレーションは、どのような戦略構成を使うかを決めるために行いました。この結果は、他の戦略を整理するのに役立ちます。
条件
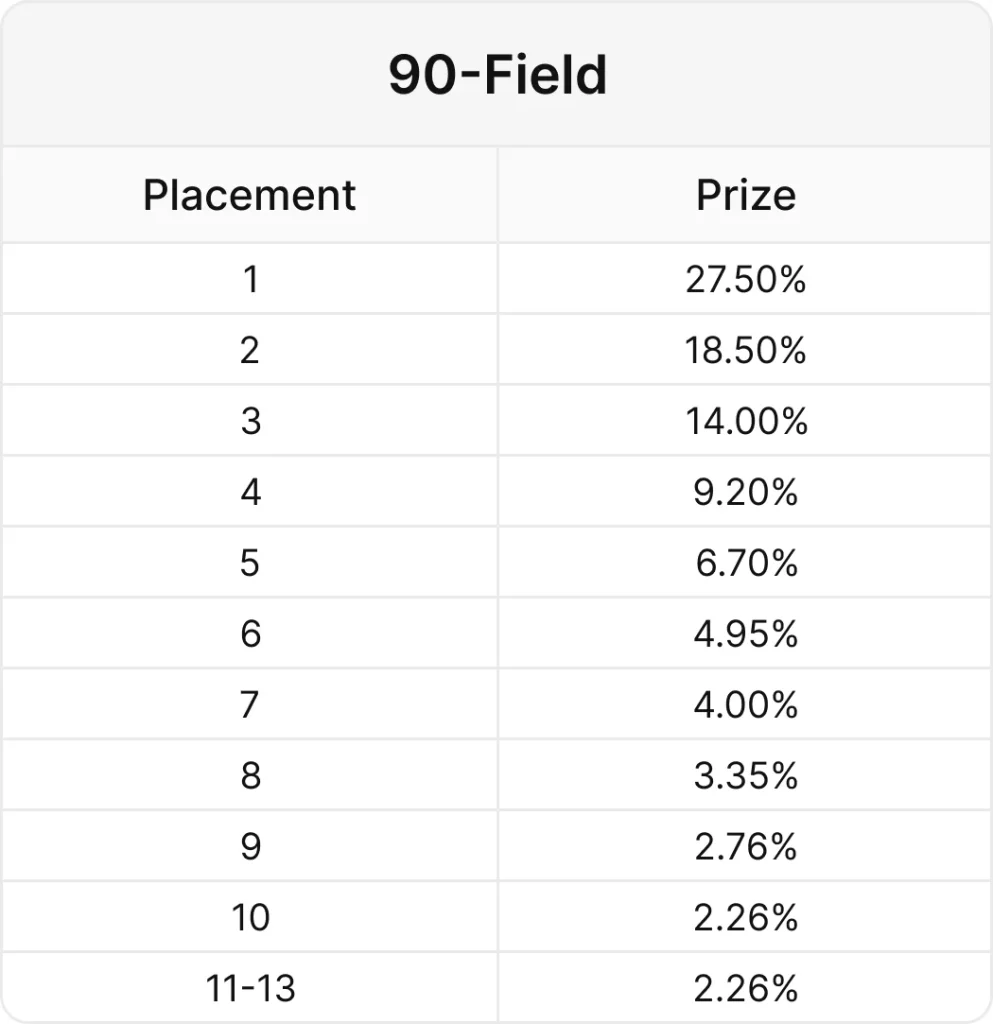
- 参加者90人のフリーズアウト
- 13人がITM
- オールインかフォールドのみ
- BBB = 平均スタックの1/7
- 9つの戦略構成
- すべてのプレイヤーはお互いの戦略を知っていて、お互いにエクスプロイトし合う。
- サンプル数 = 100,000回
戦略構成
- ICM 100%
- cEV 12.5% / ICM 87.5%
- cEV 25% / ICM 75%
- cEV 37.5% / ICM 62.5%
- cEV 50% / ICM 50%
- cEV 62.5% / ICM 37.5%
- cEV 75% / ICM 25%
- cEV 87.5% / ICM 12.5%
- cEV 100%
結果
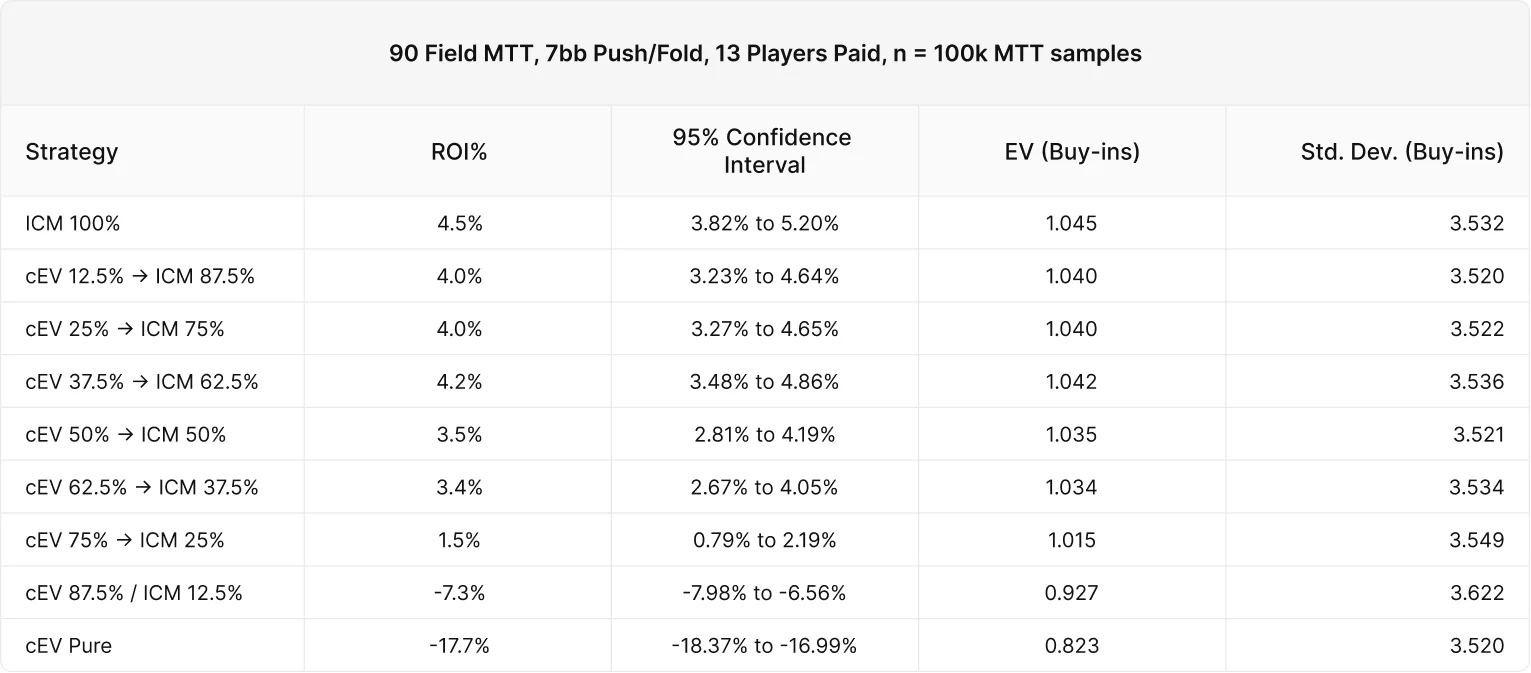
前回と同様に、ICM戦略に早く切り替えたプレイヤーの方が多くの利益を上げる傾向が見られました。
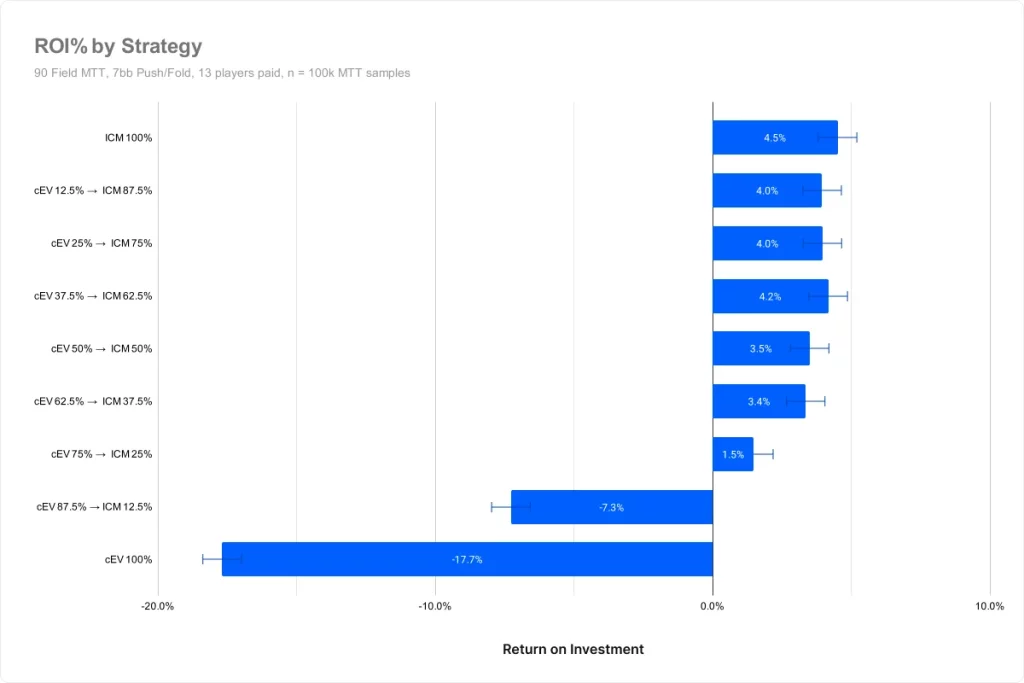
類似した戦略があるため、この結果には若干のノイズがあります。しかし、全体的な傾向は変わりません。
純粋なcEV戦略が大きく損をしているため、他の戦略構成のEVが前回の実験と比べて増加しています。これは、自分のEVが下手なプレイヤーの数によって変動することを示しています。
cEV(75% / ICM 25%)戦略よりICMが少ないと損をします。これは統計的にも明らかです。バブルは残りの参加人数が14.4%になった後ですが、25%でICMに切り替えたプレイヤーは負けています。これは、ICMがバブルよりかなり前に統計的に有意な影響を与えるという結果をさらに強化するものです。EVと順位の分析はここでは省略します。
実験4 – スタックの深さによる違い
ここまでの実験では、平均スタックはすべて7BBでした。次に、スタックの深さを5BBから10BBの間で変化させ、それがどのような影響を与えるかを見てみます。
条件
- 参加者90人のフリーズアウト
- 13人がITM
- スタックは5BB、7BB、10BBの3つ
- アクションはオールインかフォールドのみ
- 6つの戦略構成
- すべてのプレイヤーはお互いの戦略を知っていて、お互いにエクスプロイトし合う。
- サンプル数=500,000回
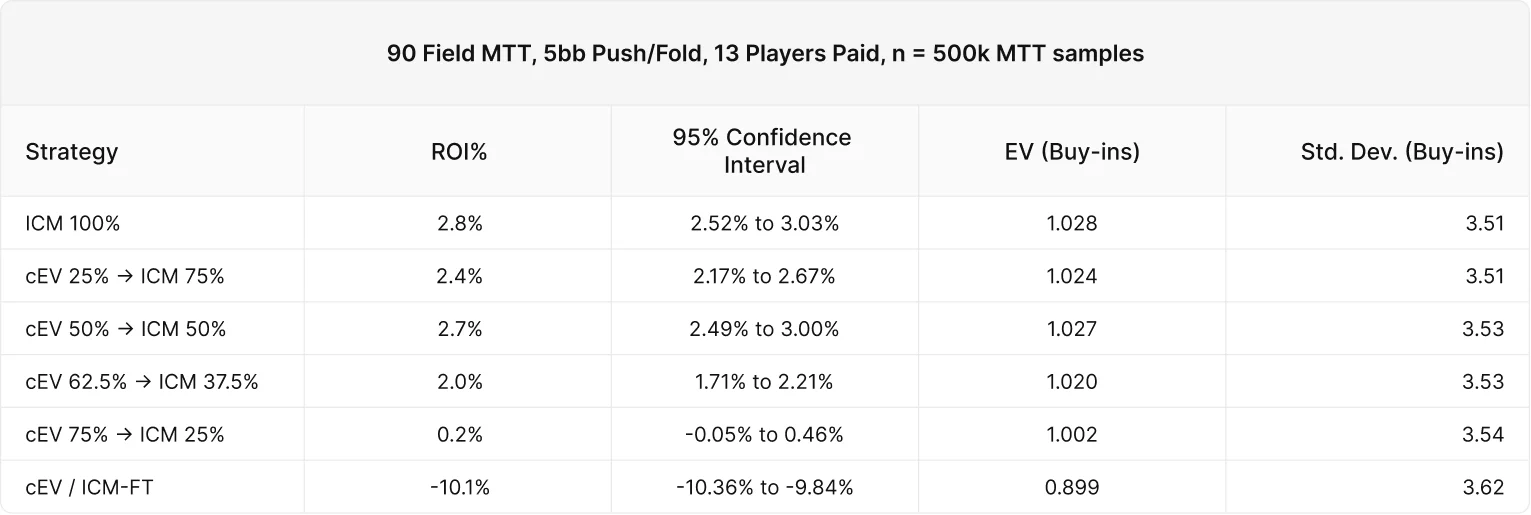
平均スタック5BB
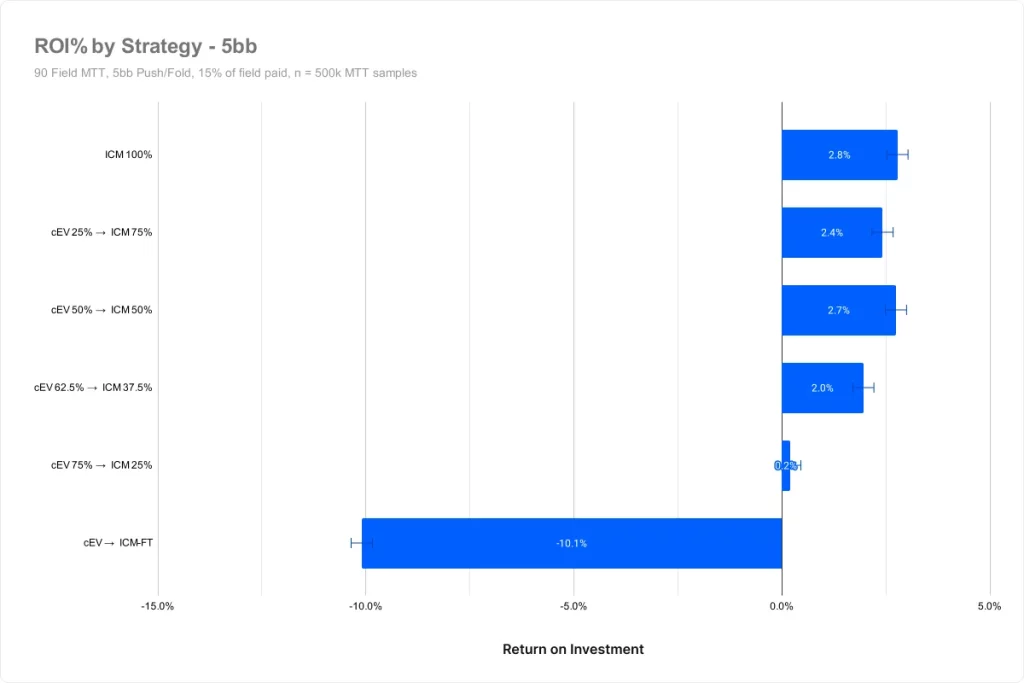
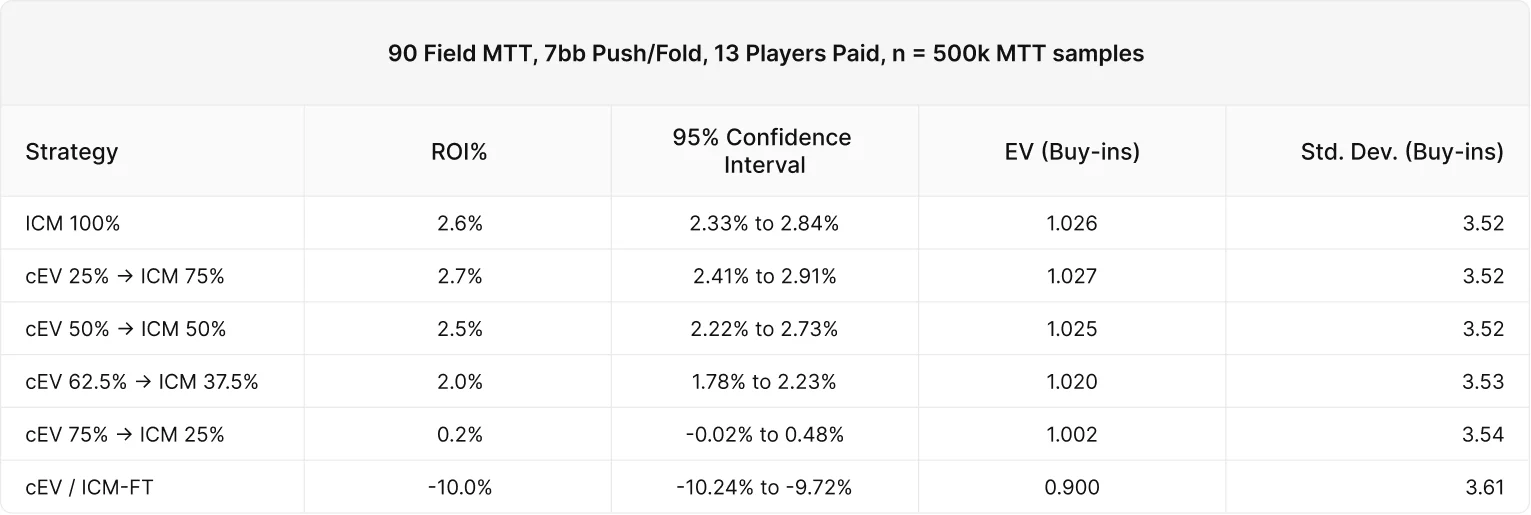
平均スタック7BB
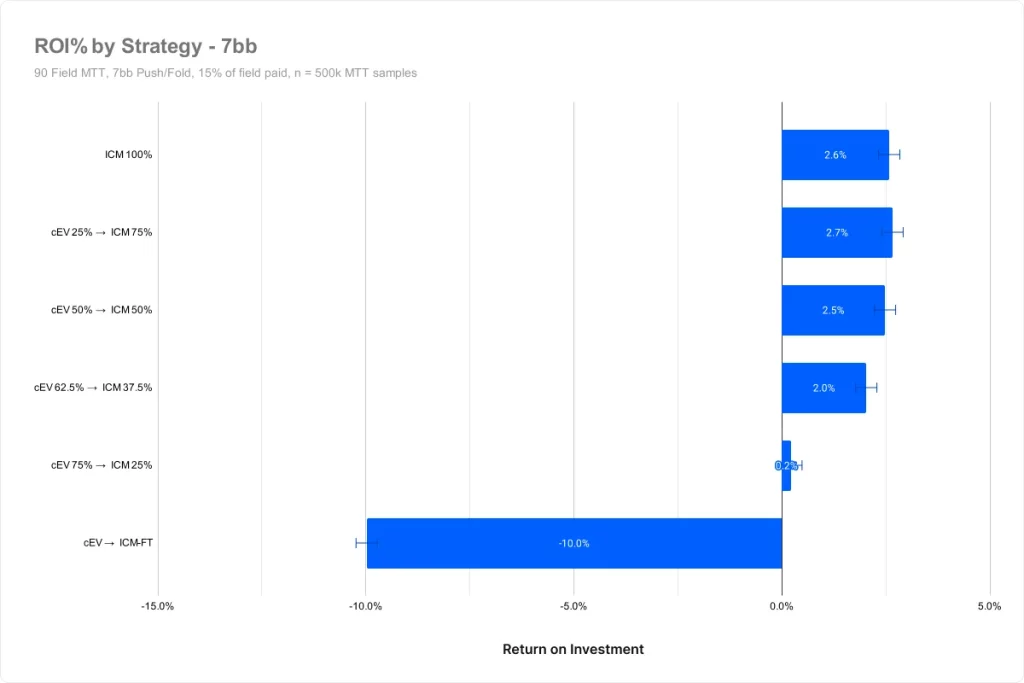
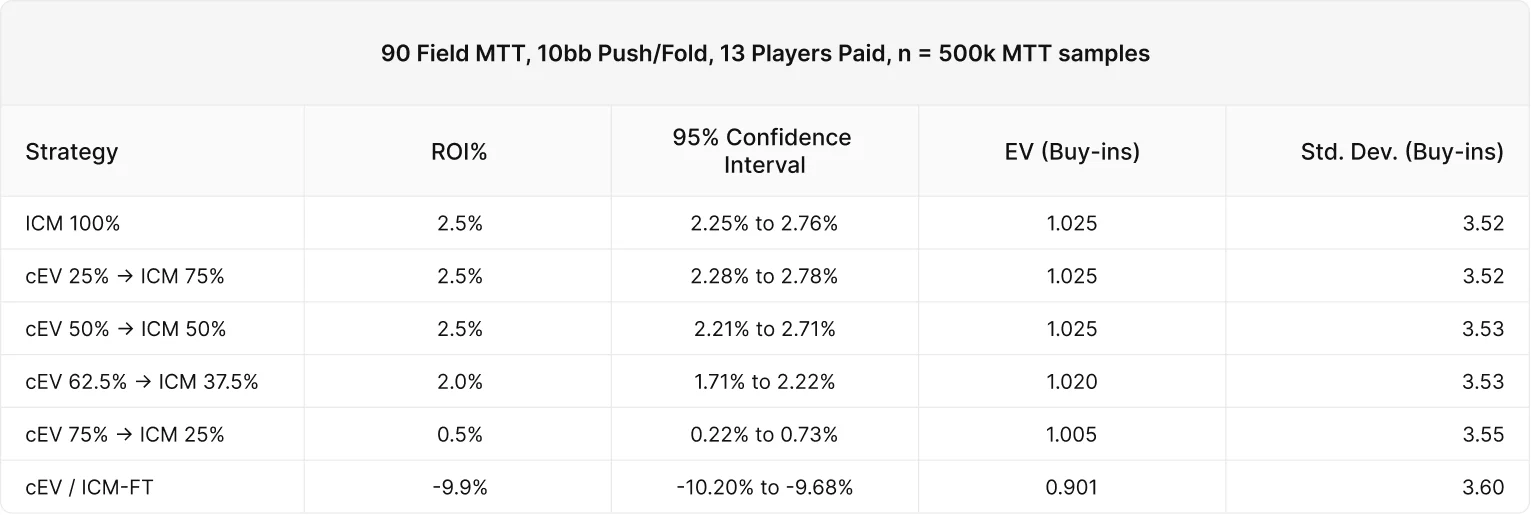
平均スタック10BB
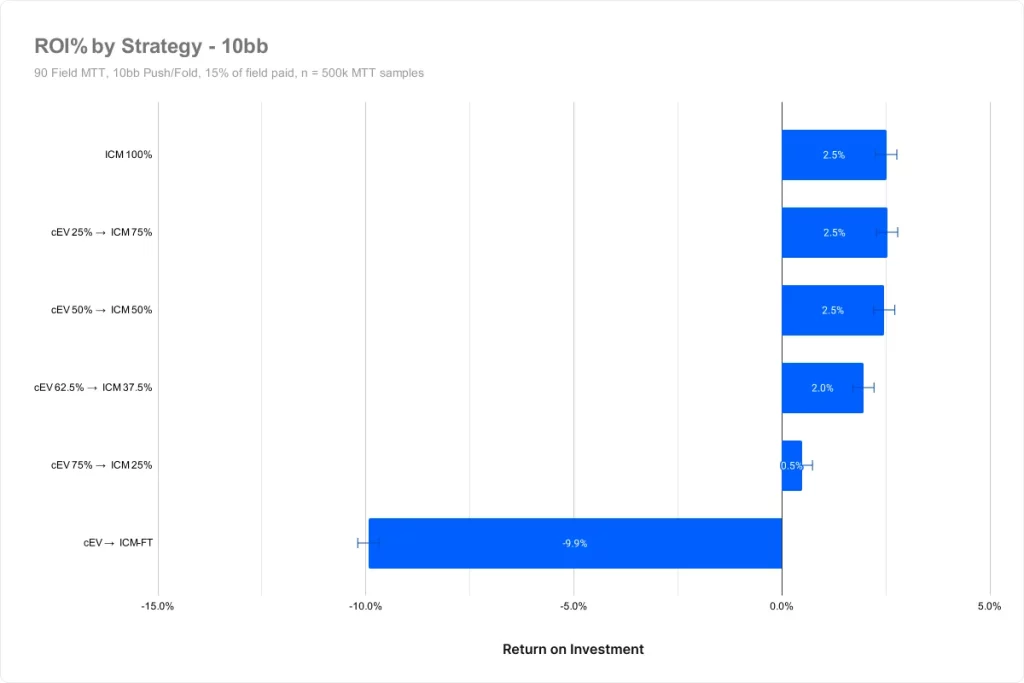
スタックの深さを変えた分析
すべてのケースで、cEV 62.5% / ICM 37.5%以下の戦略は統計的に悪い結果となっています。10BBではオールインレンジがタイトになるため、スキルエッジが少なくなっていると推測できますが、これはただの分散の可能性もあります。
実験5 – 概念の誤解について
多くのプレイヤーは、ICMをトーナメントが終わってもらえる額のように考えています。これは間違っています。スタックの価値を見積もることと、トーナメントを止めることは同じではありません。こういった誤解が生まれるのは、おそらく次の2つが原因です。
- ICMはファイナルテーブルでのディールによく使われるため。
- ICMは次のラウンドのポジションやブラインドの増加を考慮していないため。
ICMは戦略やポジションの有無や、レンジについて全く考慮しません。ICMはスタックを基準に順位の可能性を計算しているに過ぎません。
この実験を通して、プレイヤーがICMを知らない場合でも、ICMが機能することを証明します。
条件
今回は、ハーフスタックのプレイヤーとフルスタックのプレイヤーの2つのグループでシミュレーションします。どのプレイヤーもチップEV戦略を使うので、このシミュレーションでは誰もICMを気にしません。
- ハーフスタックとフルスタックの2つのグループ
- 全員がチップEV戦略をとる
- BB = 平均スタックの1/7
- 参加人数200人のMTT、上位15%がITM
- オールインとフォールドのみ
- 100ドルバイイン
- サンプル数: 250,000回
結果
ここでは、ハーフスタックとフルスタックのプレイヤーのシミュレーションの結果とICMの計算結果を比較します。
表の「Top15%」とは、トーナメントで上位15%に入る頻度を意味します。「Top50%」は、トーナメントで上位50%に入る頻度を意味します。ICMはハーフスタックのグループのトーナメントの価値を$67.74、フルスタックのグループのトーナメントの価値を$132.26と予測しています。
ではこれらの予測がシミュレーションの結果にどれだけ近いか見てみましょう。
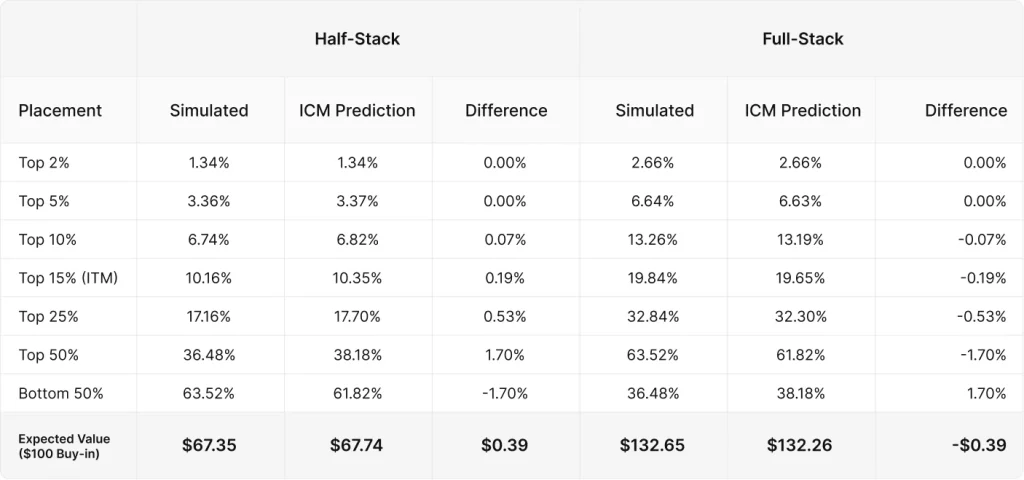
ICMが予測したEVとシミュレーションの差はわずか$0.39でした。これはトーナメントに参加するプレイヤーがICMを知っているかどうかに関わらず、ICMがトーナメントエクイティを計算する上で重要かつ正確な要素であることを示しています。また、この結果から残りの人数が少なくなるにつれてICMが正確になっていくことも分かります。
戦略への影響
この実験の目的は、ICMが重要になるタイミングを見つけることです。GTO Wizardを使ってトーナメントの中盤でも戦略が大きく変わることをお見せします。
以下のgif画像は、トーナメント全体でどのように戦略が変化するかを示しています。これは、実験1で挙げた参加者200人のペイアウトストラクチャーに基づいています。
例1: LJ RFI
20BBでのLJのオープン戦略を見てみましょう。比較を分かりやすくするため、プレイヤーは全員20BBとします。頻度はあまり変わりませんが、レンジの形が大きく変わっています。
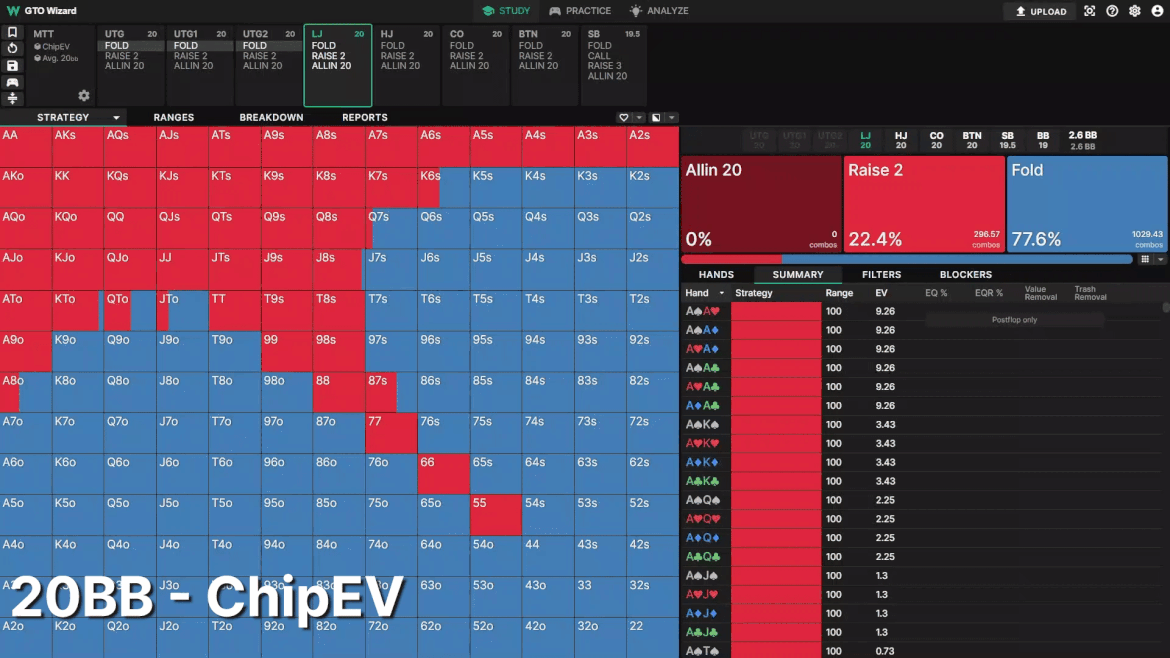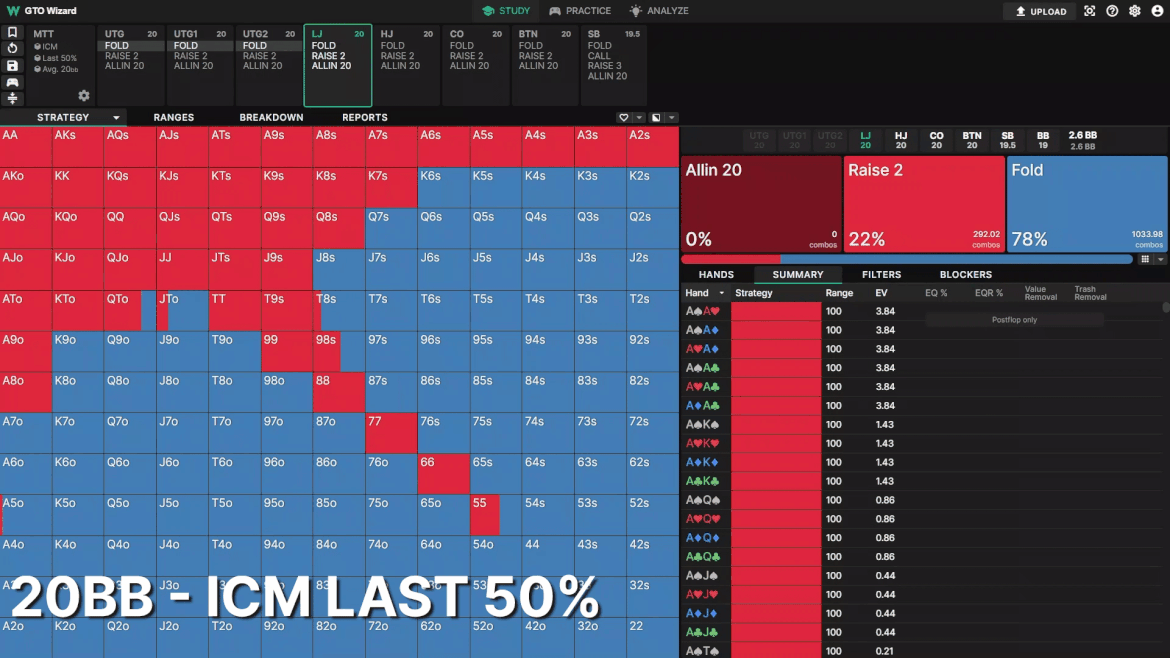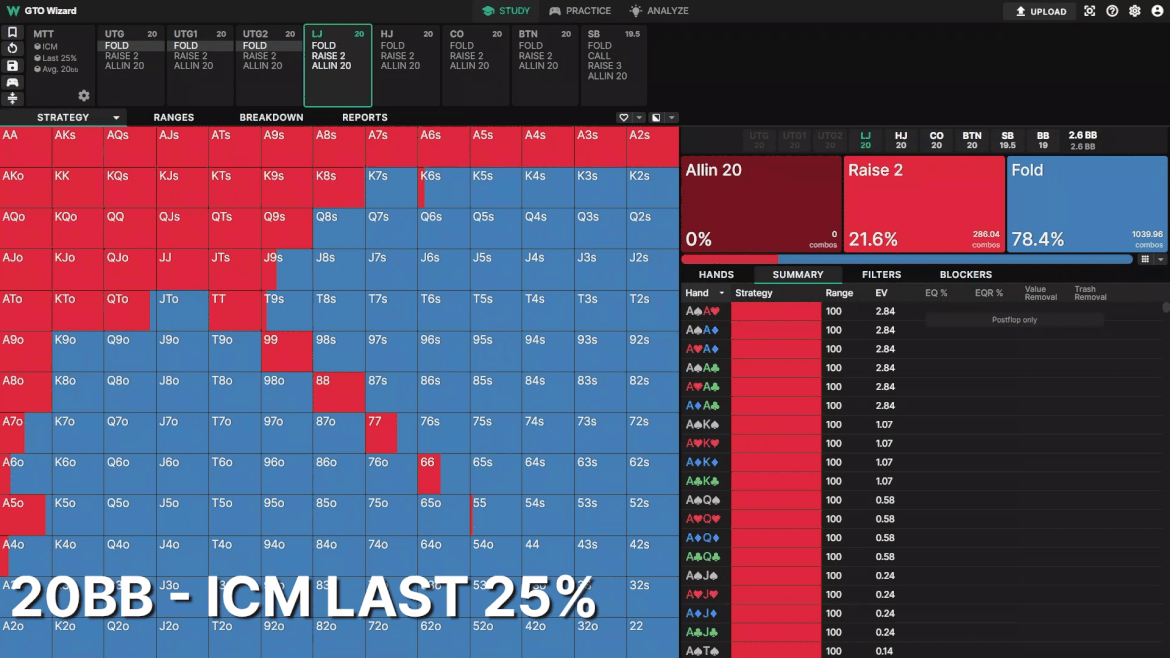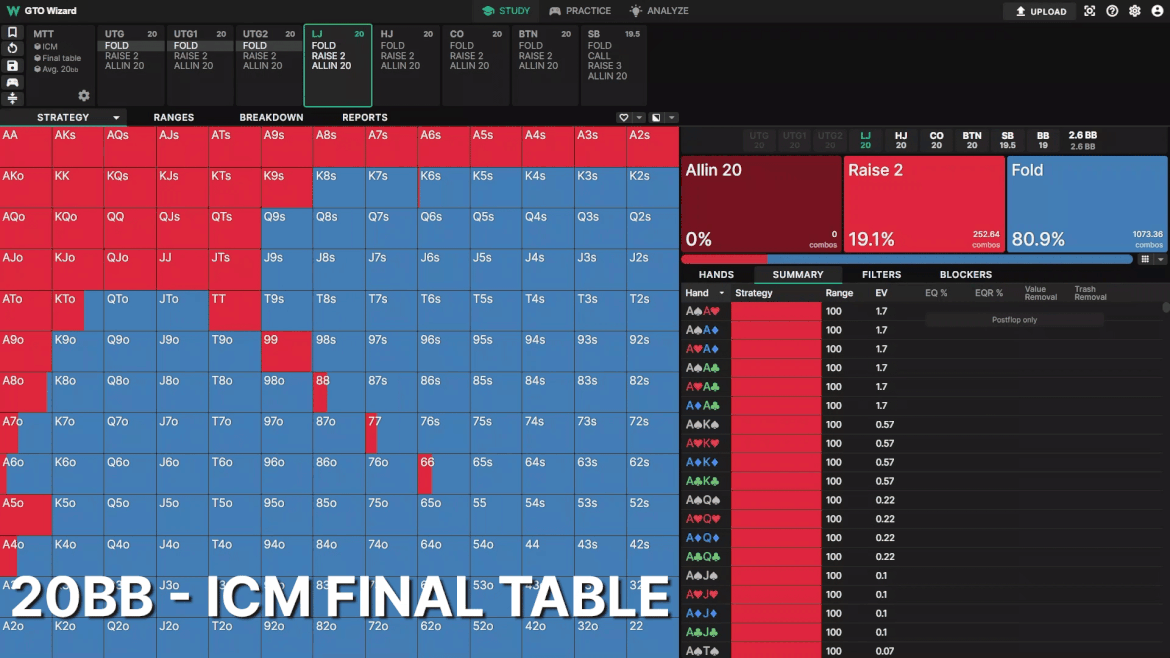
MTTが進むにつれて、オープンレンジがブロッカーに寄って行きます。リスクプレミアムが高くなるにつれ、ポストフロップでプレイするよりブラインドスチールのEVが上がります。ポストフロップのインプライドオッズは、オールインできる局面がタイトになり、リスクプレミアムが高くなったために減少します。その結果、ドローより3ベットをブロックしているハンドを評価するようになります。
例2: BBディフェンス
BBは最もICMの影響を受けます。ここでも全員のスタックは20BBとします。トーナメントが進行するにつれて、LJオープンに対してBBがどんどんタイトになっていく様子を見てください。
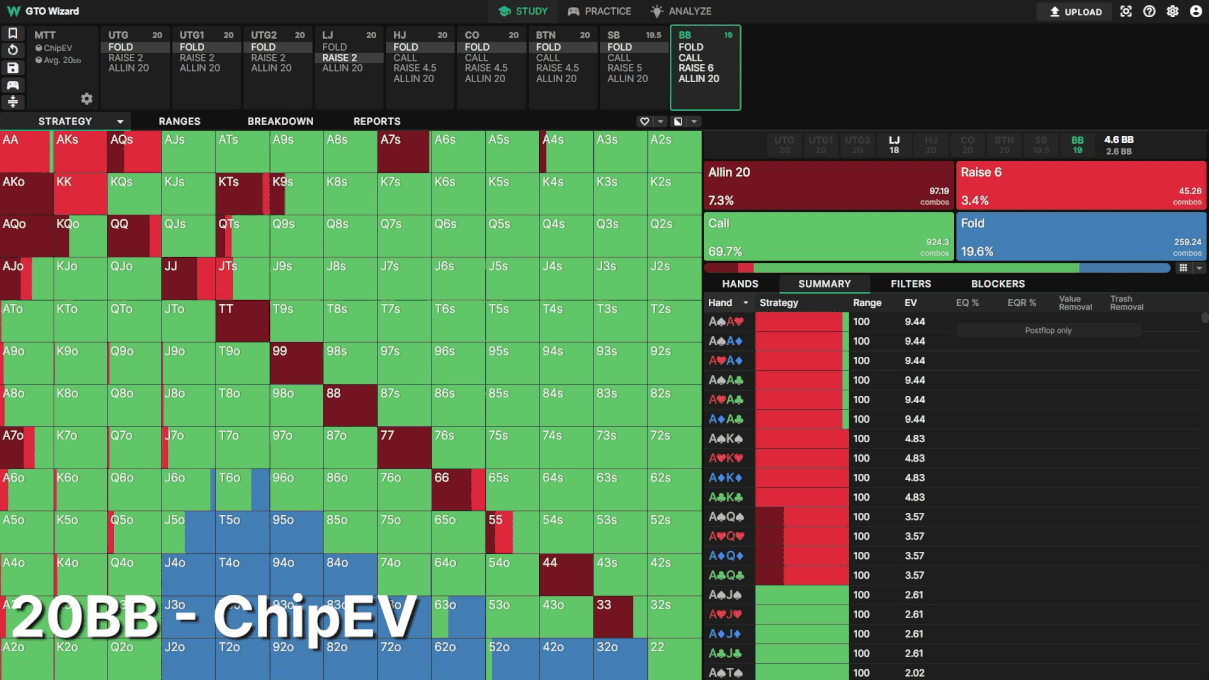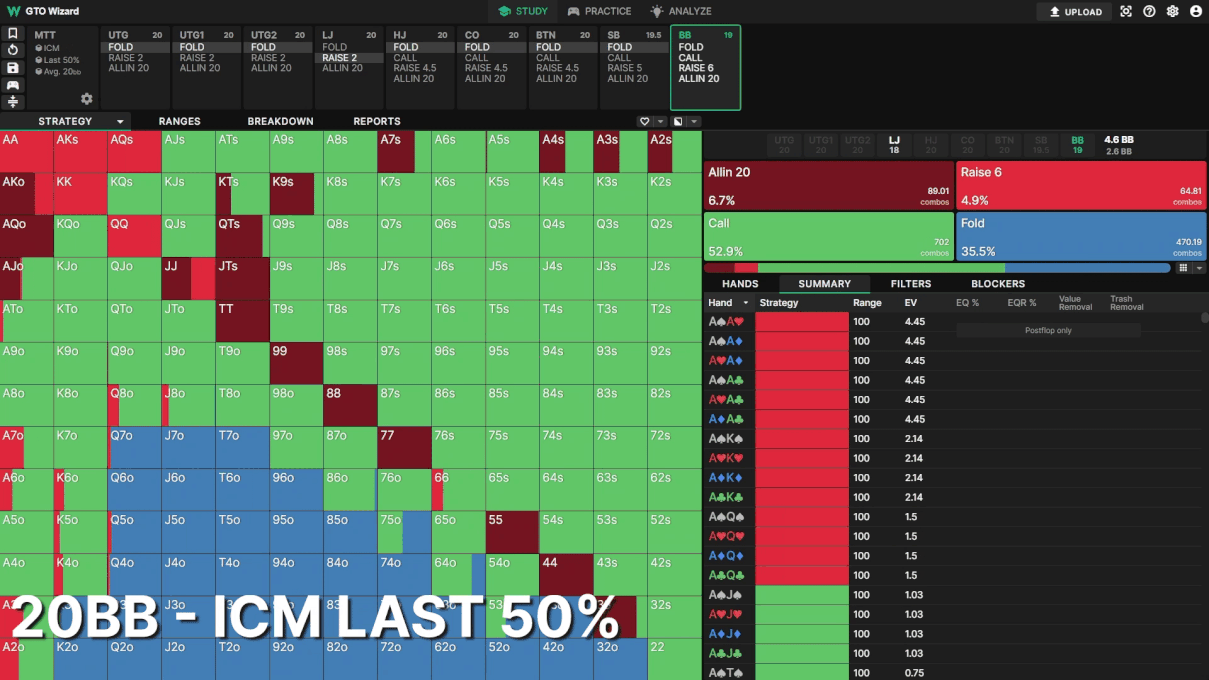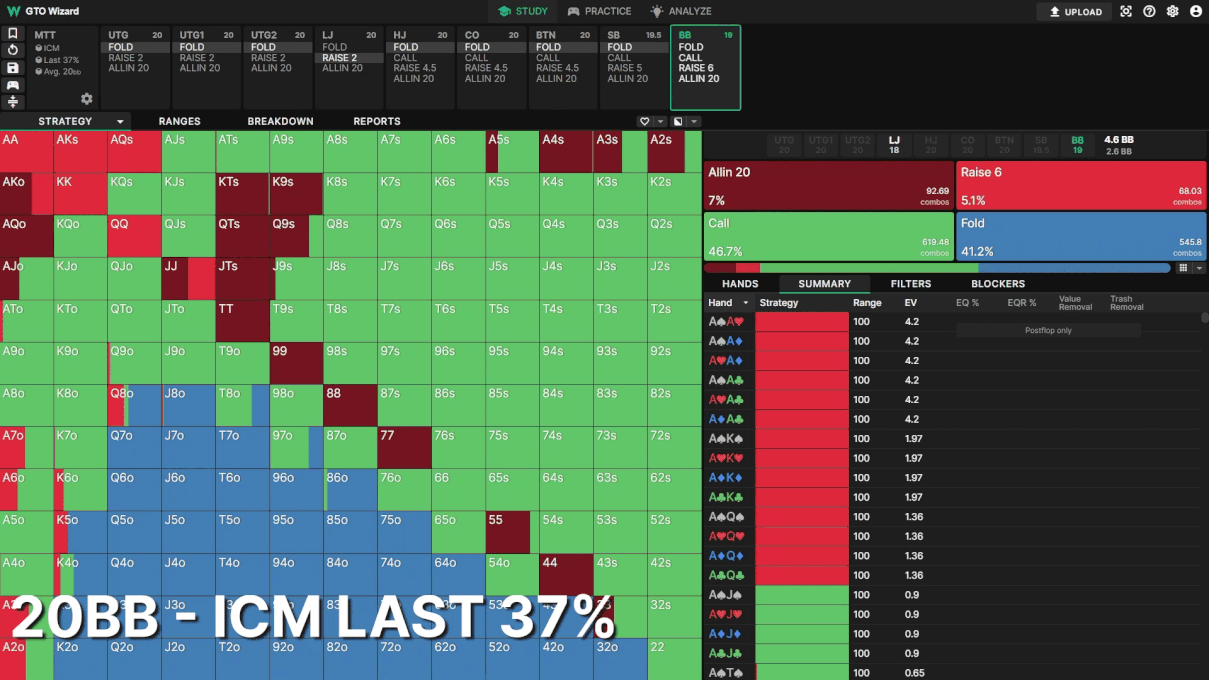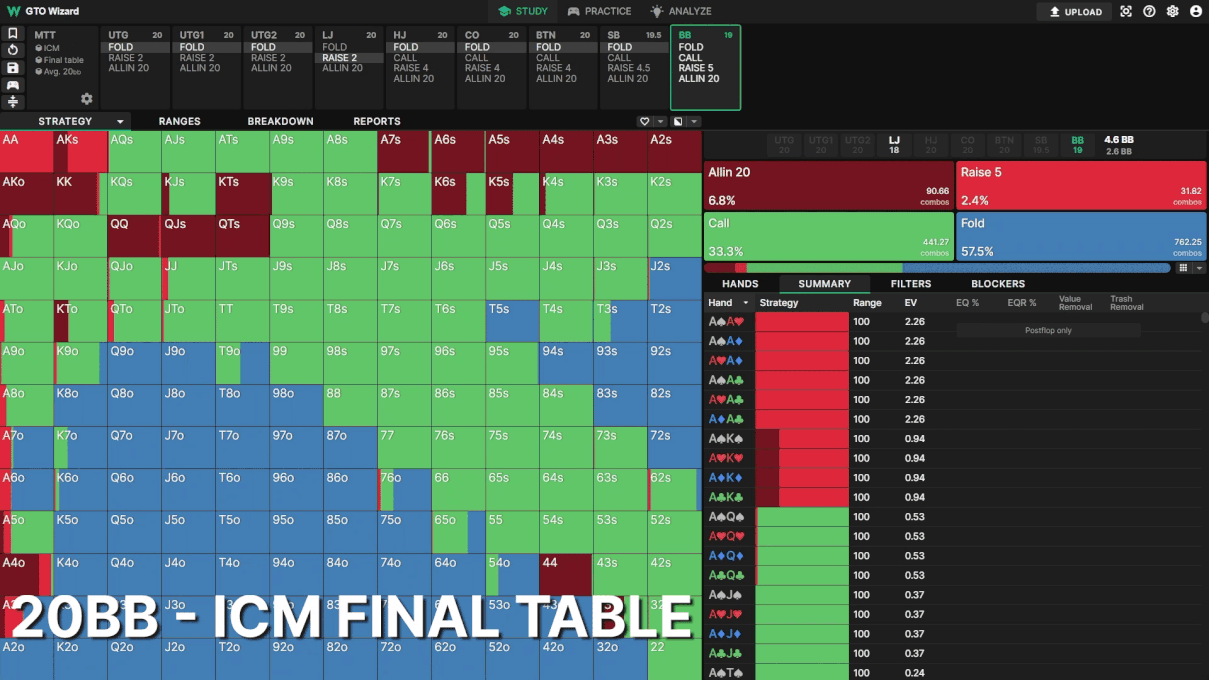
トーナメント中盤でも、BBのフォールド頻度は19.6%から35.5%に変化しています。BBのレンジのほとんどのハンドはエクイティが近いので、リスクプレミアムの小さな変化がディフェンスレンジに強く影響します。
例2: BTN 3ベットに対するLJ
LJがオープン、BTNが3ベットした局面を見てみましょう。先ほどと同様、MTTが進行するにつれて戦略は変化して行きます。
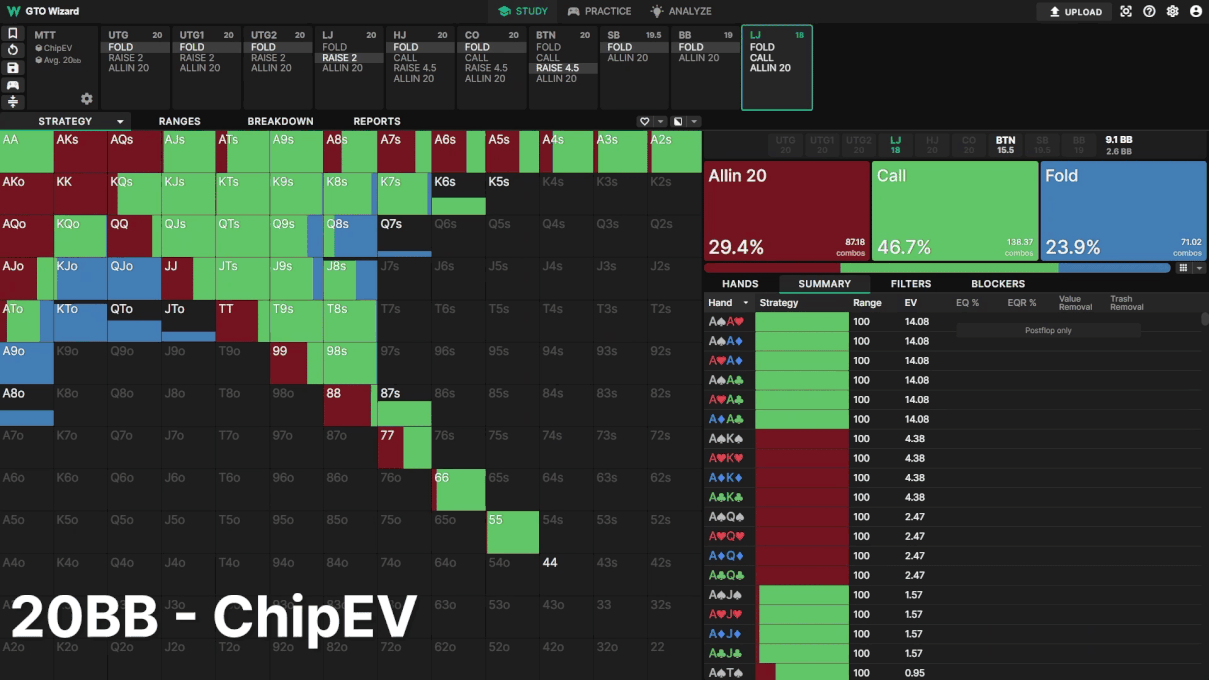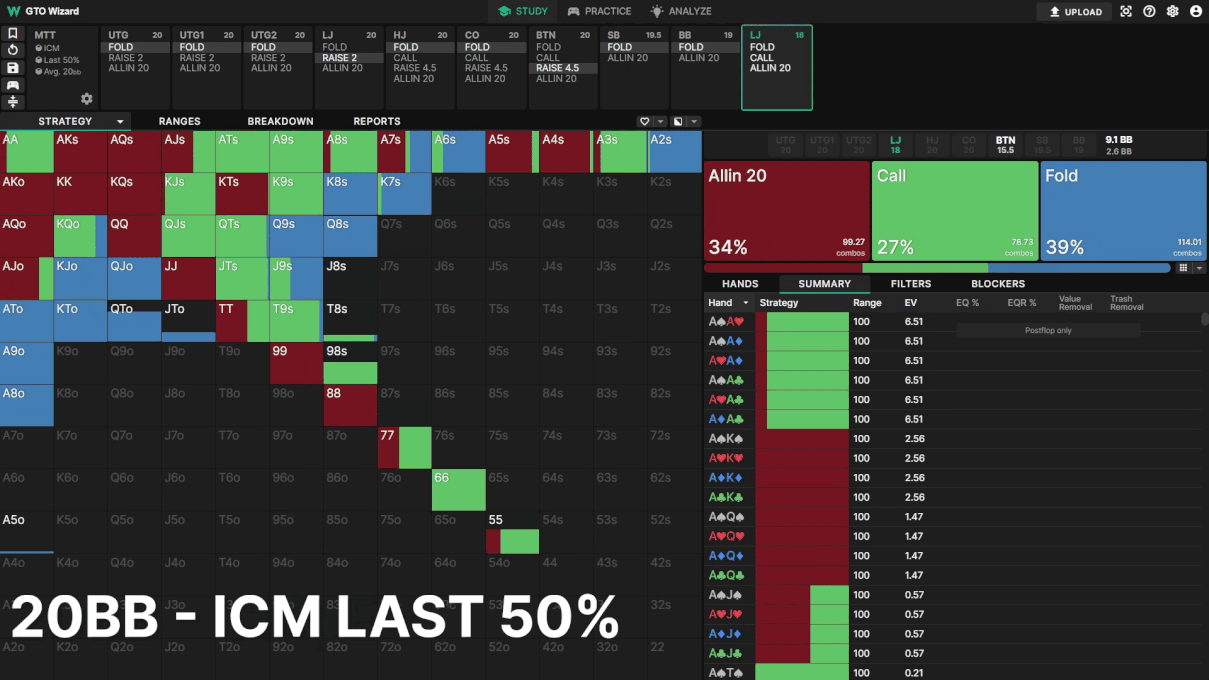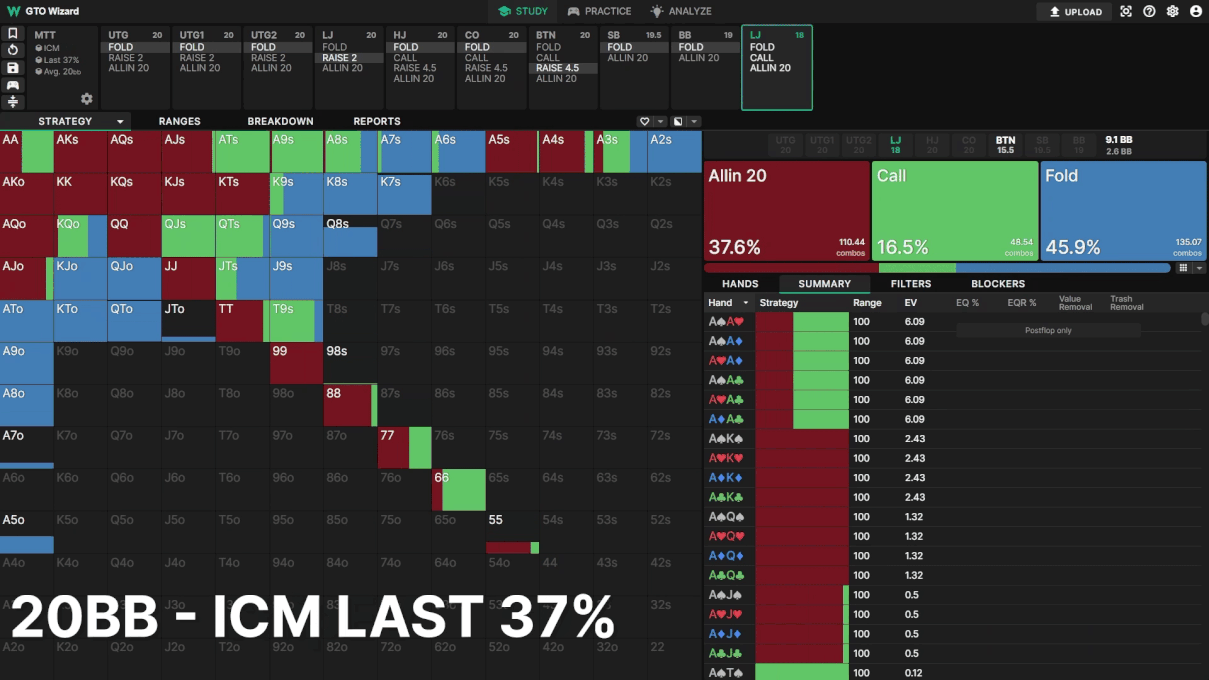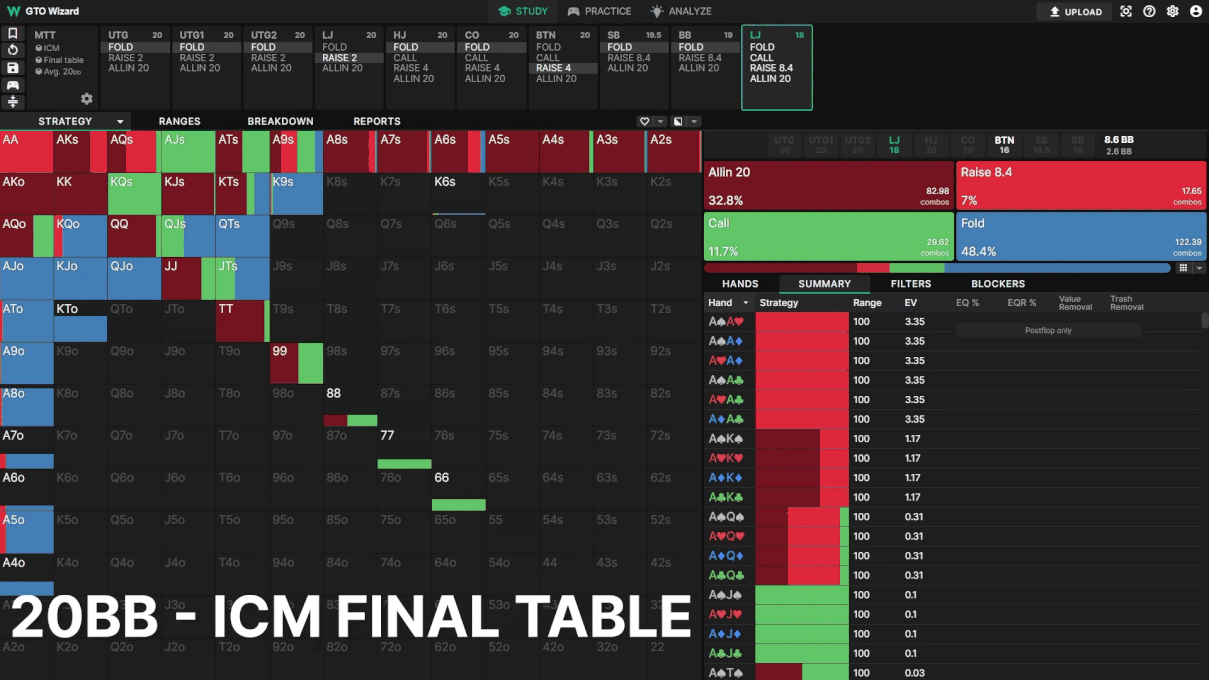
トーナメントが進行するにつれて、LJのコール頻度が減っています。その代わりに、LJはオー ルインとフォールドの混合戦略を採用し、BTNに対して「ICMを重視していること」を主張しています。ICMがプリフロップとポストフロップの戦略に大きな影響を与えることは明らかです。GTO Wizardの戦略の変化を見ると、今回のオールインとフォールドの実験は、中盤のMTTスポットにおけるICMの優位性を表しきれてはいなかったと言えるでしょう。
ICMの代わり
ICMは不完全なモデルです。より正確なトーナメント評価を強引に行うことは可能ですが、それは非常に小さなゲームツリーに限定されます。 Helmuth Melcher(Holdem Resources Calculatorの創設者)によるこの優れた論文は、従来のICMと代替モデルを比較しています。3つのトーナメントエクイティモデルをそれぞれ比較した上で、正確なNE戦略(PI-CFR+と表記)と比較しています。オリジナルの ICMの方法は「Harville」と呼ばれ、発明者の名前をとって「Malmuth-Harville」と呼ばれることもあります。
シミュレーション結果
以下の表はエクイティモデルに基づくシングルハンド均衡戦略を使うプレーヤーと、PI-CFR+戦略を使用するもう一方のプレーヤーとのシミュレーション結果を示しています。
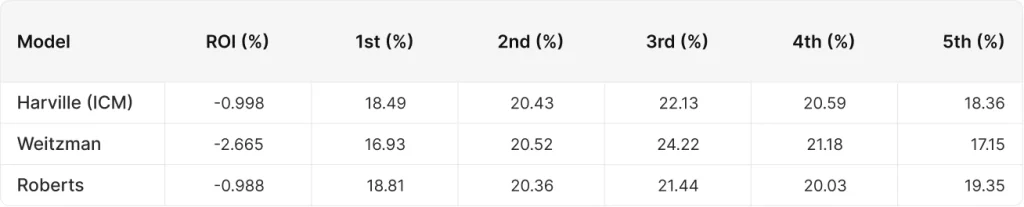
Harville (ICM)とRobertの式はどちらも非常に良い結果を出し、完璧な戦略に対して負けたのはバイインのわずか1%でした。面白いことに、Robertは完全戦略に対して負けが少ないものの、Harville(ICM)はRobertに勝っています。
我々がICMを採用する理由はより効率的だからです。オリジナルのICMは、何千人もプレイヤーがいたとしても瞬時に算出することができます!
ICMにはいくつかの制限があり、その概要はこちらで説明しています。ICMの主な弱点は、ラウンドが変わる際のブラインドの増加、ポジションやポジションの移動(FGSを使わない限り)、スキルエッジ、ポジションを無視することです。また、一般的にICMはチップリーダーのアドバンテージを過小評価する傾向があります。そうは言っても、ICMは構想から35年経った今でも非常に強力な指標です。
まとめ
今回の実験の目的は、MTTのどの時点でICMが重要な要素となるかを調べることです。これを検証するために、トーナメント中のさまざまな局面でチップEVモデルからICMモデルに切り替え、何百万ものMTTをシミュレーションしました。
- 複数のトーナメントストラクチャーと参加人数をテスト
- 複数のスタックサイズをテスト
- プレイヤーがICMを使用していない場合でも、ICMの予測能力が正しいことを証明
- MTTの途中でも、ソルバー戦略が大きく変化することを確認
今回わかったことは、早くICMに切り替えたプレイヤーの方が、後からICMに切り替えたプレイヤーよりも全てのトーナメントで良いということです。
中盤までにICMに切り替えた戦略は一貫して利益が増えましたが、その増加幅は比較的小さく、誤差の範囲内でした。ICMが統計的に有意な影響を結果に与えるのは、ITMが上位15%で残りのプレイヤーが50%から37%の間のどこかであることが、根拠を持って証明されました。ICMに切り替える「スイートスポット」は、バブルのおよそ3倍で発生すると推測できます。ICMがバブルのかなり前から戦略に大きな影響を及ぼしていることは、もう明らかでしょう。
Holdem Resources Calculator
Holdem Resources Calculator (HRC)の創設者であるHelmuth Melcher氏には、このシミュレーションを実施していただき、またこの実験中にご指導をいただきました。
私たちの意見では、HRCは最高のICMツールであり、大規模なMTTのICMを瞬時に計算できる唯一のソルバーです。ICMの実験にご興味のある方は、2023年1月22日までHRCの無料トライアルをご利用いただけます。