トイゲームの解き方

トイゲームとは、ポーカーを簡略化したもので、ゲーム理論を学ぶ際によく使われています。

ポーカーは非常に複雑なゲームなため、GTO戦略を人間が自力で計算するのは不可能です。ただし、トイゲームを使用することで計算を簡略化でき、GTOの基本的な要素を学ぶことができるようになります。

この記事ではいくつかの基本となるトイゲームを紹介しますが、それを知ったからといってすぐにトッププロになれるわけではありません。しかし、ソルバーへの理解度はより深まるでしょう。

この記事では、トイゲームの基本となるポラライズ対ブラフキャッチャーについて紹介します。

基礎的な知識

トイゲームを理解するにはまず、ポットオッズ、MDF、期待値の計算の方法など基礎的な知識が必要です。

• MDFを知ることで、相手のブラフのEVをゼロにするためには、どれくらいの頻度でコールするべきかがわかります
• ポットオッズを知ることで、コールする際にどれくらいエクイティが必要か、またブラフとバリューの比率をどれくらいにすべきかわかります
• S = ベット/ポット

計算方法がわからない人は、下記の記事をご覧ください。

• MDF
• ポットオッズ
• EV

下記のシートを使うとすぐに計算できます。

ポラライズ対ブラフキャッチャー

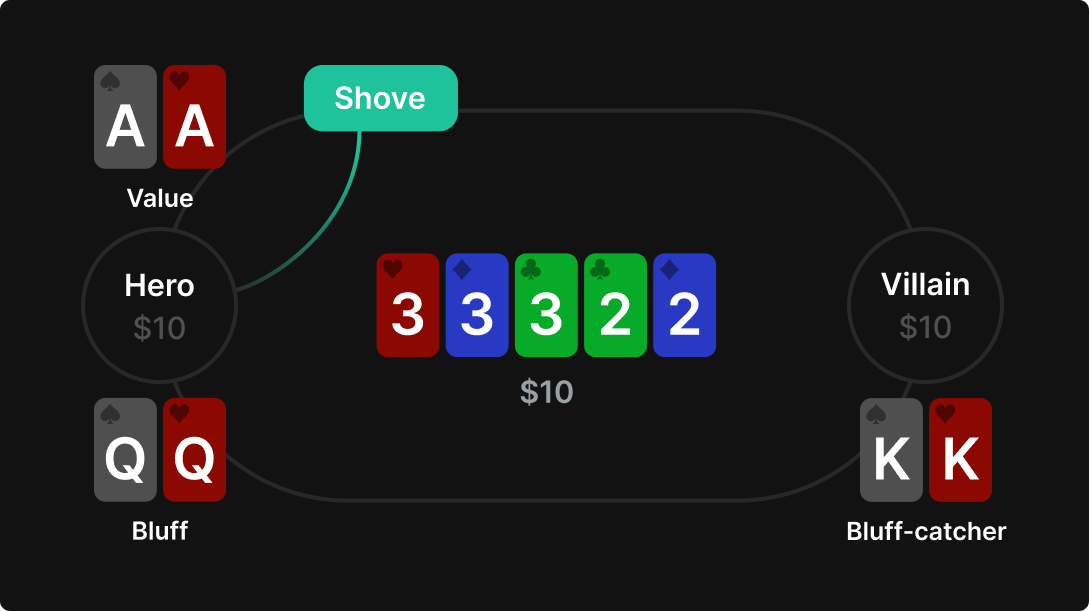
ポラライズ対ブラフキャッチャーのトイゲームは、片方のプレイヤーがナッツとブラフ（エクイティ0％）を持ち、もう一方がブラフキャッチャーを持っているという状況でのゲームです。

• プレイヤー1（最初にアクション）：AAとQQを同じ割合で持つ
• プレイヤー2：KKだけを持つ
• ボード：22233
• ポットとスタックは10、アクションはオールインかチェックのみ

プレイヤーは互いに相手がどのレンジでプレイしているか知っているとします。

どのようにプレイすればよいのでしょうか。4つのステップに分けて考えます。

1. 支配戦略を考える
2. ポットオッズを用いてブラフとバリューの比率を計算する
3. MDFを用いてコール頻度を計算する
4. 方程式を一般化する

ステップ1) 支配戦略を考える

プレイヤー1がチェックをしたら、プレイヤー2（KK）は毎回チェックをします。KKでベットしてもQQにフォールドされ、AAにコールされるためKKでベットをすることはありません。プレイヤー1はAAを持っている時は毎回ベットをするべきです。

ステップ2) ブラフとバリューの比率を計算する

AAは毎回ベットすることはわかっていますが、QQはどのくらいの頻度でベットするべきでしょうか？QQのブラフ頻度が多いと、プレイヤー2は毎回コールし、逆にブラフ頻度が少ないと、プレイヤー2は毎回フォールドし、エクスプロイトしてきます。エクスプロイトされないように、プレイヤー2がコールとフォールドどちらの戦略をとってもEVが変わらないようにベットをします。

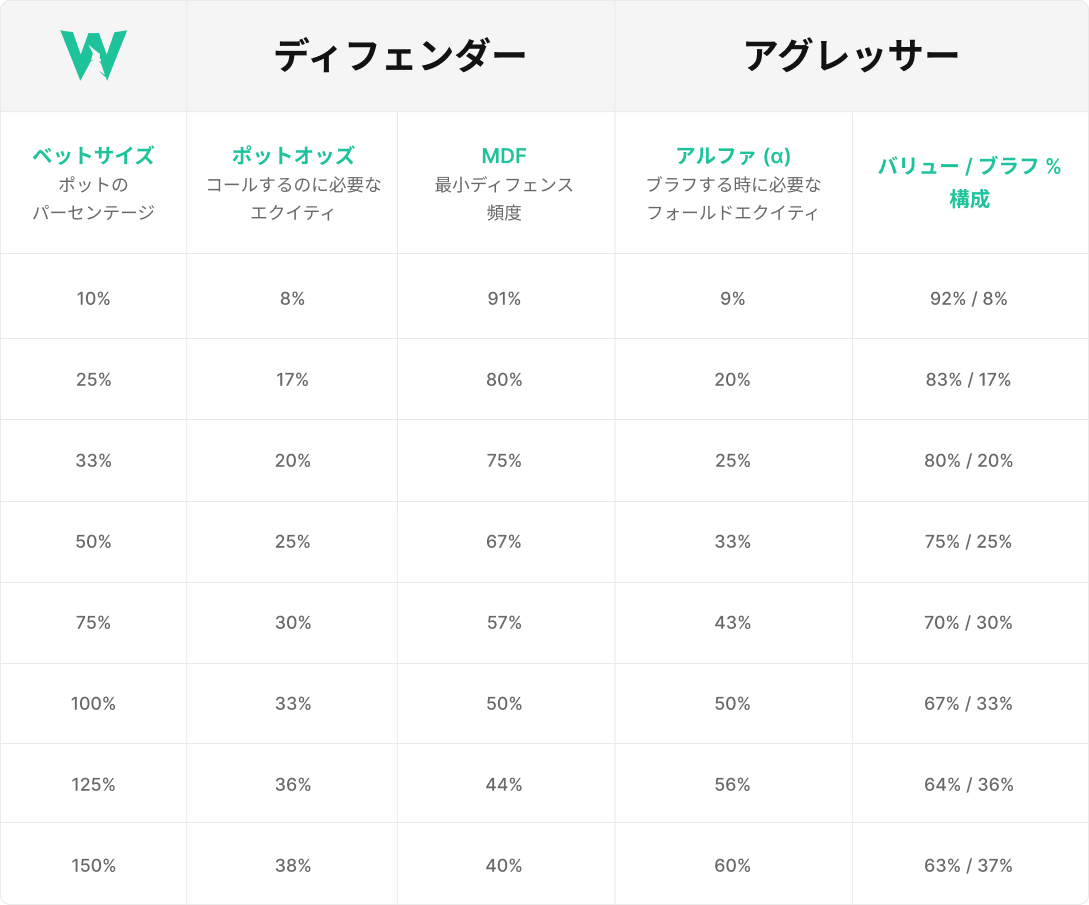
ポットサイズのベットなので、コールするには相手は33%のエクイティが必要です。

必要なエクイティ = （コールの額）/（コール後のボット額） = 1/3

つまり、ベットレンジのうち、1/3はブラフにしなければいけません。AAは全てベットするのでQQは半分ベットして、相手に2:1のオッズを与えると、相手はエクスプロイトできなくなります。

Step 3) KKのコール頻度を計算する

フォールドし過ぎると、ブラフを多くされ、コールし過ぎるとブラフを少なくされてしまいます。そのため、相手のブラフがチェックとベットでEVが変わらないようにコール頻度を調整しなければいけません

MDFを使ってKKのコール頻度を求めます。コール頻度はベットサイズによって変化します。

MDF = ポット / (ベット + ポット) = 1/2

KKは2回に1回コールするべきです。

まとめると、AAは毎回、QQは2回に1回ベットし、残りのQQはチェックします。KKは2回に1回コールし、残りはフォールドします。チェックされた場合はチェックバックをします。

Step 4) 一般化する

ベットサイズやバリューとブラフの比率が違ったらどうなるでしょうか？このトイゲームでは、ベットサイズが重要な関数となってきます。

s = ベット/ポットとします。

• AAは毎回ベット
• 相手に適正なポットオッズを与えるようQQをブラフ
• MDFに従ってKKはコール

MDFをsを使って表すと、KKのコール頻度 = 1/(1+s)
必要なエクイティ = s/(2s+1)

ベットされた時のKKのエクイティは、ブラフの割合と等しくなります。

ブラフ/（バリュー＋ブラフ）= s/(2s+1)

問題

下記の条件の際、それぞれのプレイヤーの均衡戦略はどのようになるでしょうか。

ポット = 10、ベット = 7
プレイヤー1は AAを5コンボ、QQを6コンボ
プレイヤー2はKKのみ

解答を見る前に、まずは自分で計算してみてください！

ポラライズ vs ブラフキャッチャー（トラップあり）

先ほどのポラライズ vs ブラフキャッチャーのトイゲームの計算方法がわかったところで、次はトラップ(バリューハンドより強いハンドのこと)がある場合について考えてみましょう。

前提条件

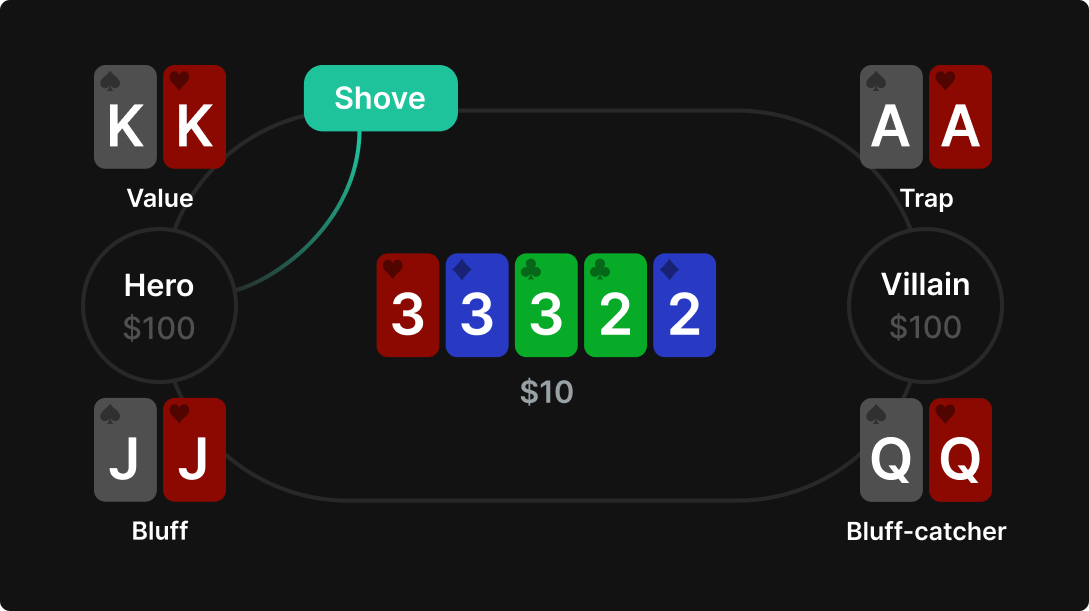
リバーで相手が22233ボードでチェック、相手のレンジの90%はブラフキャッチャー、10％がトラップです。自分のレンジは50%がバリューで残り50％がブラフです。

相手 (OOP)：90% QQ, 10% AA
自分 (IP)：50% KK, 50% JJ
ボード： 22233
ベットサイズは好きに選べます！
相手はコールもしくはフォールドのみです。

相手がトラップを持っていなかったら、一番悪いオッズを与えるためオールインをしますが、このトイゲームでは、相手の一部のハンドは自分のバリューハンドよりも強く、ベット額を大きくしてしまうとそのハンドにチップを多く取られてしまいます。ただ小さくし過ぎるとバリューを取り逃してしまいます。

このトイゲームでは、ベットサイズ理論の基本原理が働きます。

完璧なベットサイズはどう考えたらわかるのでしょうか。

トイゲームを解いてみよう

s = ベット/ポット
t = 相手のレンジにあるトラップの割合
q = コールされたときの自分のエクイティ
c = 相手がコールする頻度

ステップ1）相手がどれくらいコールするかを考える

相手はベットされた時、MDFに従ってコール頻度を決定します。

コール% (c) = Max( MDF, トラップ%) = Max(1/(1+s), 10%)

つまり、コール頻度はMDFに従いますが、トラップの割合である10％を下回ることはありません。

相手がMDFに従ってコールしているのでブラフのEVは常に0です。

ステップ2）コールされたときのバリューハンドのエクイティを計算する

バリューハンドはトラップには負けるため、コールされた時のバリューハンドのエクイティを計算して期待値の方程式を導きます。

コールされた時のエクイティはベットサイズによって変化します。ベットサイズが大きくなればなるほど相手はブラフキャッチャーを多くフォールドし、それに比例してコールレンジの中のトラップの割合が増えます。つまり、バリューハンドのエクイティ(q)は相手がコールするブラフキャッチャーとトラップの割合と等しくなります。

コールされたときのエクイティ＝コールレンジ内のブラフキャッチャーの割合＝（コール頻度-トラップの割合）／コール頻度
q = ((c-t) / c)

ステップ 3) 期待値を計算する

ベットした時の期待値を表す方程式を考えます。最適なベットサイズを用いると、EVを最大化することができます。

相手はMDFに従ってコールするため、ブラフのEVは0です。（大きなサイズでベットをするとマイナスになる可能性はありますが今回は考慮しません）自分のEVに0を加えたとしても何も変わらないため無視できます。

ブラフハンドのEVはありませんが、バリューハンドのEVはあります。

EV(バリューベット) = コール%(コールされたときのEV) + フォールド%(ポット)
EV(バリューベット) = コール%(勝率 * (ポット + ベット) – (負ける確率 * ベット)) + フォールド%*ポット

変数に置き換えます。

• ベット% = s
• ポット = 1 (s = ベット/ポットであるため、1とします)
• コール％ = c
• 勝率と負ける確率 = qと(1-q)

EV（バリューベット） = c(q(1+s) – s(1-q)) + (1-c)

ここにqを代入することもできますが、解析したいわけでなければ必要ありません。

EV（バリューベット） = 1+s(c-2t) – t

ステップ4) ベットサイズによる期待値のグラフ化

最適なベットサイズを見つける一番簡単な方法は、ベットサイズによる期待値をグラフにして最も高い点を見つけることです。

グラフを見てみましょう。トラップの数に応じてベットサイズとEVをグラフ化できるものを作成しました。tスライダーをドラックすると数値がわかります。

この関数では、相手が10％のトラップを持っている場合、最適なベットサイズは123％ポットサイズであることがわかります。ただ100％から150%の間ではほぼ同じEVです。

分析的なソリューションを欲しい方もいると思います。それには微積分が必要です。EVを最大化するargmax（最大点集合）’s’を求めます。ただEVをグラフ化して最適なベットサイズを求める方が簡単であるとは思いますが一応式を紹介します。

動画もご覧ください

この動画では、他の種類のトイゲームについても触れています。

• ポラライズ vs ブラフキャッチャー
• ポラライズ vs ブラフキャッチャーとトラップ
• ドローでのブラフ
• 複数ストリートにまたがるポラライズゲーム
• 01ゲーム

本でより深く知る

トイゲームを学ぶことでゲーム理論をより深く理解することができ、実践でより良いプレイができるようになります。今回紹介したトイゲームは数あるトイゲームの中での一部にしか過ぎません。

トイゲームについてもっと知りたい方は以下の本をおすすめします。

• Expert Heads Up No Limit Hold’em, Volumes 1 & 2 by Will Tipton
• Play Optimal Poker, Volumes 1 & 2 by Andrew Brokos
• Modern Poker Theory by Michael Acevedo
• Mathematics of Poker by Chen & Ankenman