分散とバンクロール管理

全てのポーカープレイヤーに必要なソフトスキル

ポーカーテーブルでより多くの利益を出すために私たちは努力しますが、ポーカーの本質はギャンブルです。ポーカーは勝てるゲームですが、他のカジノゲームと同じように気が狂いそうになる分散の上に成り立っています。

動画を見る

ポーカーは運かスキルか

ポーカーは運かスキルなのかは、プレイするハンドの数次第です。小さなエッジ、つまり実力者と初心者のスキルの差は、長期的に見れば大きくなります。短期的には、ポーカーの勝敗はほとんど運に左右されます。しかし、長期にわたってプレイすると、小さなエッジも必然的に大きくなります。ポーカーは短期的にはほとんど運ゲーですが、長期的にはスキルの差によって勝敗が決まります。

分散とは

分散とは、データセットの数字間のばらつきを統計的に表したものです。ポーカーでは、分散は勝敗の結果がどれだけ「揺れ動く」かを意味します。

分散が大きいゲームでは、プレイヤーの結果が、与えられたサンプルの中で期待値から大きく外れることがあります。

分散は「標準偏差」で計算されます。標準偏差は、HUDで見ることができますが、プレイした結果から直接計算することもできます。キャッシュゲームでは、BB/100 ハンドで表されます。

いくつかの例を見てみましょう。以下のグラフはランダムな20パターンの例です。 (出典　Primedope)

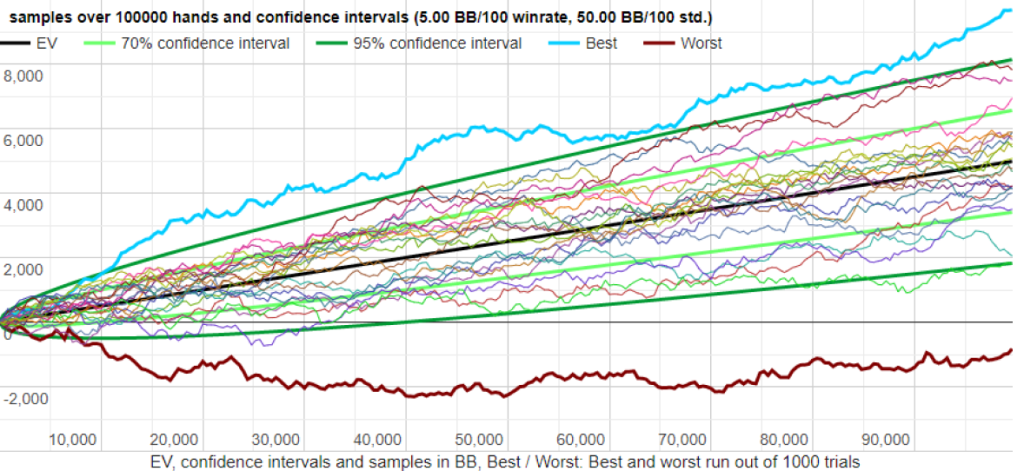
分散が小さい場合

最も良いケースと悪いケースで、-1,000 BBと+10,000 BBの開きがあります。

分散が大きい場合

最も良いケースと悪いケースで-17,000から+22,000の開きがあります。

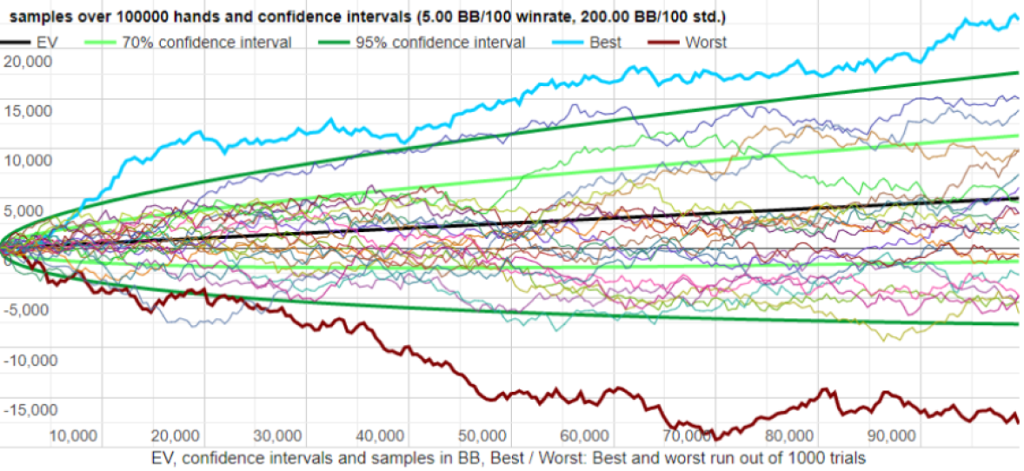
どちらのプレイヤーもウィンレートは同じですが、分散の大きいプレイヤーの方が、最も良いケースと悪いケースとの値の差が大きくなります。

大数の法則

ギャンブラーがよくする勘違いは、ポーカープレイヤーも陥りがちです。仕掛けのないコインを投げて、6回連続で表が出たとします。次に裏が出る確率はどのくらいでしょうか？

迷信深い人なら、裏が出る確率が高いと思うかもしれません。しかし、実際はそうなりません。次のコインの裏表の確率は50%対50%です。7回目に表が出る確率は、1回目に表が出た確率と同じです。

何千回もコインをひっくり返せば、表も裏も均等になるはずです。しかし、この現象は普遍的な法則ではなく、単なる大数の法則によるものです。1000回投げて、表が503回、裏が497回と表が6回多く出ているとします。それが期待値となります。この時点で、表が50.3%、裏が49.7%です。

ここで、10万回ひっくり返して、同じく6回出る回数に差があるとします。今度は50.0003%で表、49.9997%で裏が出たことになります。裏が出た回数は決して表の回数と同じではないものの「運」は平等に感じられます。これが大数の法則です。

同じように、運が悪かったからといって、今後「運が良くなる」というわけではありません。出るカードはあなたとは無関係なのです。それぞれのハンドは独立した事象であり、AAをまくられた記憶には左右されません。

逆の場合もまた有り得ます。運が良かったからといって、必ずしも不運がその後に訪れる訳ではありません。実際、ポーカーにおける分散は、人間の頭で考えられる範囲をはるかに超えています。ポーカーの分散を勉強した人であれば、統計的に意味のあるエッジが出るまでには何万ものハンドが必要なことを理解しているでしょう。

信頼区間

よくある質問に、「自分のウィンレートを確証するためには、何ハンド必要なのか」というものがあります。この問題の難しい点は、確実な答えがないことです。この問題を明らかにするために、数学では信頼区間を用います。

信頼区間は68-95-99の法則に従います。

分散分布

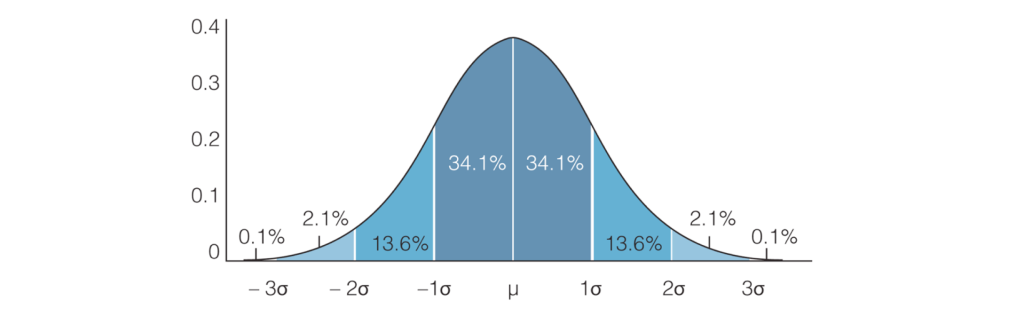
例を見てみましょう。

平均したウィーンレートが2.5BB/100ハンドだとしましょう。このウィンレートが期待値となります。
10万ハンド後の標準偏差(σ)は3.16 BB/100ハンドです。
ウィンレートをより正確に記述すると以下のようになります。

2.5 ± 3.16 BB/100(ウィンレート ± σ)

言い換えると

数学においては、確定していない変数は正確な数値としては扱わず、許容誤差や信頼区間を利用します。ウィンレートは確定していない変数です。したがって、正確な数値を出すことは不可能です。ある程度の許容誤差を求めるのが良いでしょう。

許容誤差の式は、標準偏差とハンド数で成り立っています。ハンド数を増やすか、分散を小さくすれば、誤差が小さくなり、結果の信頼性が高まります。計算式は以下の通りです。

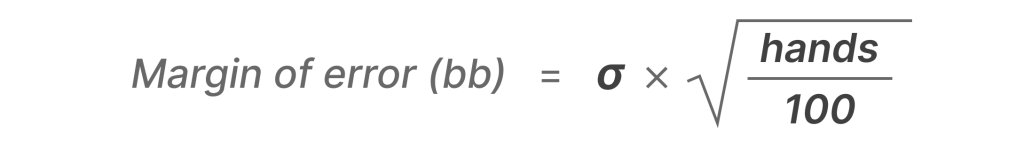
σは標準偏差（BB/100）で、handsは単純にプレイしたハンドの数です。上の例では、標準偏差が100BB/100で、10万ハンドをプレイしたとします。100 x (100,000/100)^0.5 = 3162となります。計算結果は±3162BBとなり、100ハンド当たり3.16BBとなります。この計算結果は「10万ハンド後の標準偏差」として算出されましたが、許容誤差と考えた方がわかりやすいでしょう。

リスク管理

分散は前述の入力したデータに基づいて、無料のソフトで計算することができます。

お勧めのウェブサイトはPrimedopeとReviewPokerRoomsです。分散を理解することは、結果と期待値の関係性を正しく理解することに繋がり、重要だと言えます。様々なデータを試し、その結果を見ることが大切です。

上記のツールはキャッシュゲーム用です。MTTではさらに大きな分散が起こりやすいです。このMTT用のツールをお試しください。

バンクロール管理のガイドライン

この記事の目的は何らかの絶対に正しい答えを教えるのではなく、バンクロール管理の方法を確立する上で、役立つツールを紹介することです。BRM（バンクロール管理）はどの程度リスクをとるかによりますが、以下に一般的なBRMの目安を記載します。

キャッシュプレイヤー　35〜65バイイン

• バンクロールの5%以上を賭けない

トーナメントプレイヤー　 75〜125バイイン

• バンクロールの2%以上を賭けない

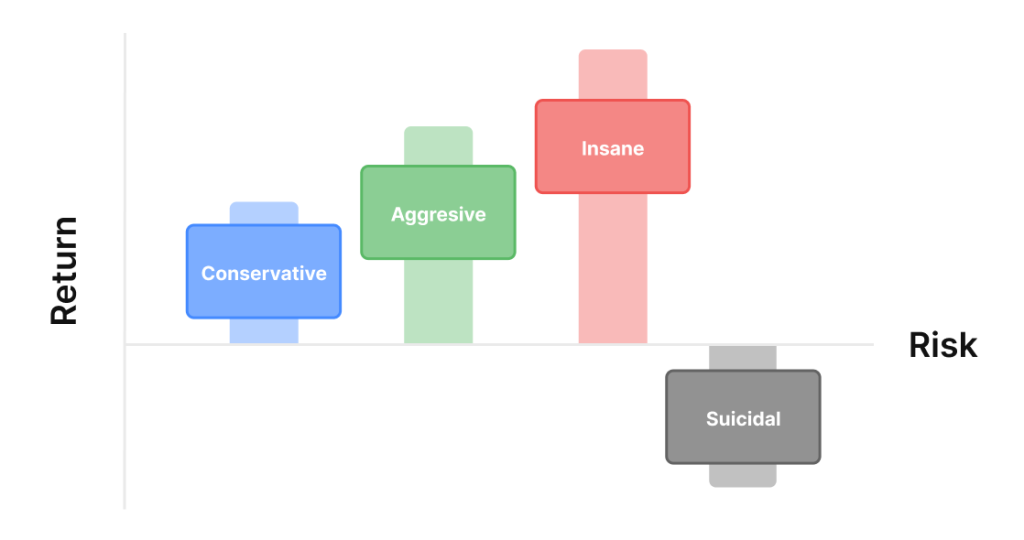
ケリー基準

ケリー基準は、バンクロール全体のうち、どれくらいをリスクにさらすべきかを考える上で役立ちます。エッジとオッズを踏まえて、バンクロール全体のどれくらいをリスクにかけるかを計算できます。

「バンクロール管理で最も重要なことは、自分のコントロール可能な範囲内でエッジを最大化することです。これはケリーが実際に行ったものです。」

ケリー基準の計算式は以下の通りです

f = ベットするバンクロールの割合 b =10進数のオッズ – 1 p =勝率 q = 負ける確率を表す1 – p

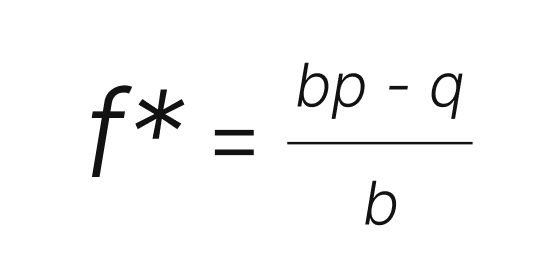
  例を見てみましょう

ヘッズアップHUSnGをプレイし、平均投資収益率（ROI）は5%です。
バンクロールは1000ドルです。
できるだけ早くバンクロールを増やすには、どのステークスでプレイすべきでしょうか？

A) 100ドルバイイン
B) 50ドルバイイン
C) 25ドルバイイン
D) 10ドルバイイン

最適なバンクロール管理とは

ケリー基準を用いることで、バンクロールの内どのくらいをリスクにさらすべきかを算出することができます。しかし、どれくらいのリスクを取るべきかはウィンレートと分散によります。ケリー基準は判断基準の1つであり、常に正しい訳ではありません。実戦ではケリー基準よりも少ない額になります。

数学を用いつつ、キャッシュゲームや他のポーカーのゲームでのウィンレートから最適なBRMを導き出すことができます。BRMの計算機を使うことで、効率よくステークスをあげていくことができるでしょう。💪

この計算機を使えば、1時間当たりのウィンレートを上げるよりも、ステークスを上げて、より大きな分散をくらった場合にも対処できる最低限のバンクロールを計算できます。

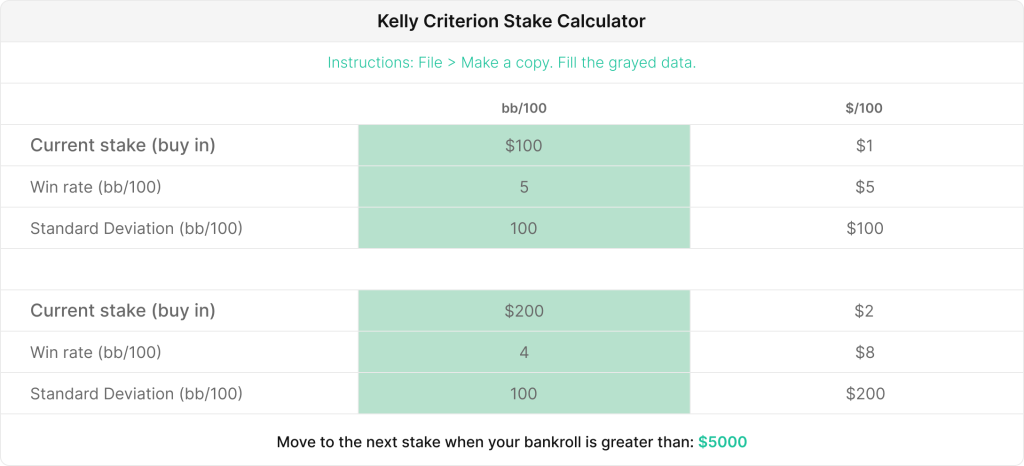
また、MTT用にベータ版の計算機も用意しました。ケリー基準は、トーナメントなど様々な要素があるゲームでは複雑になってしまいます。バンクロールに大きな変化をもたらす結果もあれば、非常に小さな影響しか与えない結果もあります。

この式を利用して、MTTにおける最適なBRM戦略を求めてみます。

この式では

実際にはこの式に値を代入することはかなり難しいですが、ある程度のエッジ（ROI）があれば確率を見積もることができます。マルチテーブルトーナメントでは100回バイインできるバンクロールが必要だという考えは、大規模なトーナメントではあまりにも行き過ぎた考えです。

ティルト

ティルトとは、感情的になり合理的ではないアクションを取ることです。多くのプレイヤーは、負けが込んでいるときに、これ以上資金を減らしたくないと怖がったり、以前の負けを取り戻したいと思ったりして、ティルトに陥ってしまいます。

上記のように、ウィンレートが下がると分散が大きくなるので、ティルトは非常に危険です。根拠のない思い込みが実現するという自己成就予言となり、ダウンスイングの期間が長くなってしまいます。

ティルトの対処法については、後の記事で詳しく説明します。

まとめ

ポーカーの分散性から言えることは、「失う余裕のないお金でギャンブルをするな」という古くからの考えが正しいということです。

分散を学べば、アップスイングとダウンスイングは一時的に過ぎないことを理解できます。短期的にどんな結果になっても感情的にならず、ポーカーの腕を上達させていって欲しいです。